最尤推定

尤度モデルは、曲線の式になります。確率を表す曲線です。

その曲線の極大点は、「もっとも起こりやすい事」という意味になります。微分すると、極大点が求まりますが、これは「最尤推定」や「最尤法」と呼ばれます。

最尤推定は、尤度モデルを使って、未知のパラメタの値を求める方法です。

例

表が出る確率をpとします。

表、裏、表、裏、裏となった場合の尤度は、以下になります。

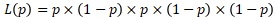
整理すると、以下になります。

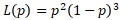
グラフで表すと滑らかな曲線です。

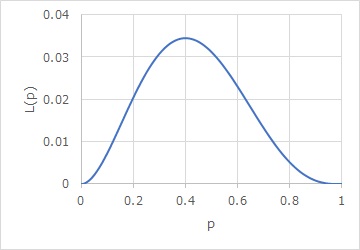
pで微分します。

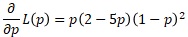
極値は、pが0、1、0.4の時です。0.4の時は、グラフから極大値で最大値になっています。

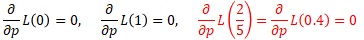
この事から、「p = 0.4」と推定できます。

表１を1、裏を0とすると、1が2回、0が3回なので、(1+1+0+0+0)/5 = 0.4でｍ平均値は、0.4です。最尤推定と、平均値が同じになることがわかります。

データが、3.5、2.2、3.3だったとします。それらは、正規分布を仮定します。母平均がμ、母分散がσ2です。尤度は、以下になります。

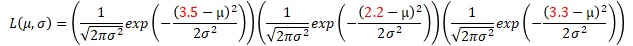
μ、σ、L（尤度）の３変数のグラフを作ると以下になります。３変数のグラフはわかりにくいので、同じデータで２種類作っています。

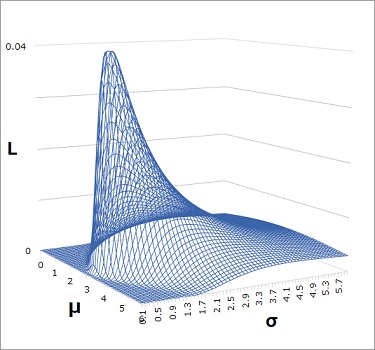
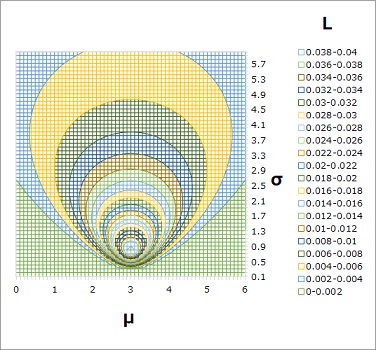
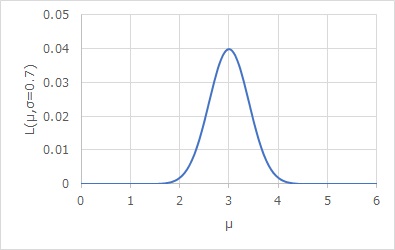
上の２次元のグラフは、σが0.7の時の断面図ということになります。

σを0.7に固定して、グラフを描くと、以下のようになります。

これを整理します。

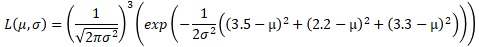
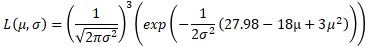
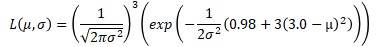
μで微分します。

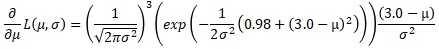
極値は、μが3.0の時です。3.0の時は、グラフでも極大値・最大値になっていることがわかります。

3.5、2.2、3.3の平均値は、3.0です。最尤推定と、平均値が同じになることがわかります。

σ2でも計算は同様ですが、最尤推定で求まる値と一致するのは、標本分散です。

上記のように、最尤推定をすると、点推定と同じ値が求まります。

「入門はじめての統計的推定と最尤法」　石村貞夫, 劉晨, 石村光資郎　著　東京図書　2010
最尤法の専門書です。正規分布と二項分布の最尤推定が、丁寧に解説されています。

「道具としてのベイズ統計」　涌井良幸　著　日本実業出版社　2009
最尤推定が簡潔に紹介されています。

「統計科学の基礎　データと確率の結びつきがよくわかる数理」　白石高章　著　日本評論社　2012
正規１標本モデルでは、σ2の最尤推定値が、標本分散であり、不偏分散(n-1で割って求める分散)ではないことの説明があります。