サンプル数が１の場合、ヒストグラムや、散布図にしても、「点が１個」というグラフになります。 標準偏差は、サンプル数は計算できません。
いわゆる「分布」というようにして、データの広がり方はわからないです。
一方、サンプル数が１だとしても、尤度関数は、広がりのあるグラフになります。
データが、3.5、2.2、3.3だったとします。 それらは、正規分布を仮定します。母平均がμ、母分散がσ2です。 尤度関数は、以下になります。
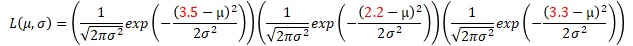
正規分布の尤度関数は、サンプル数が３の時は、３つの関数の積になっています。
そのため、サンプル数が１でも、同じように式が作れます。
下のグラフは、データが「3.0」の１個しかない場合です。
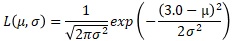
μが3.0の時は、σの逆数になり、σが０に近付くと無限大に発散します。
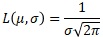
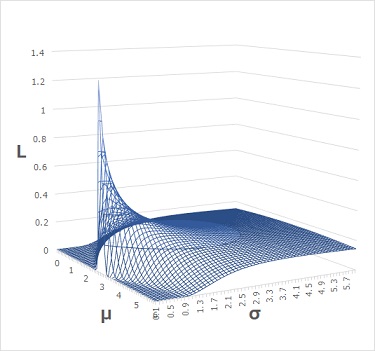
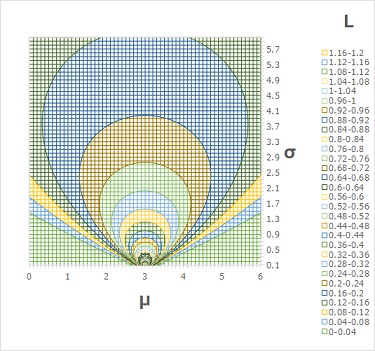
「σが０に近付くと無限大に発散」という点については、サンプル数が１という特徴が表れています。 この点から、たしかにサンプル数が１であることがわかります。
面白いのは、それ以外の部分が０になっていないことです。 これが物理的や、現実的という見方をした時に、どういうことなのかは思い当たらないのですが、興味深い性質です。
統計学の教科書では、「〇〇分布はこういうものです。式はこうです。」というようにして、分布の説明があります。
「サンプル数が１の尤度関数がある。サンプル数が複数の場合は、それらの積になる」という観点での分類は、 見かけませんが、尤度統計学では、大事な観点です。
「In All Likelihood Statistical Modelling And Inference Using Likelihood」 Yudi Pawitan 著 Oxford University Press 2013
N=1の場合の、尤度関数の説明があります。
また、様々な分布の尤度関数が紹介されています。
順路
次は
正規分布の尤度関数のサンプル数依存性
