ゼロ尤度関数

シンプルな尤度関数のページで、正規分布の対数尤度について、シンプルな式を導いています。

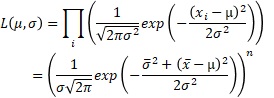
この式のかっこの中には、サンプル数nが含まれないです。そこで、以下のような式が作れます。

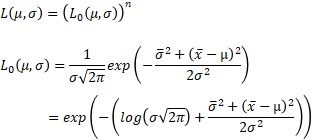
L0の部分は、サンプル数に依存しないです。

L0の式の２行目は、シンプルな尤度関数のページにある対数尤度を、指数関数に戻すことでも作れます。

この式は、筆者がシンプルな尤度関数のページを作っている中で、気付いたものです。先行研究があれば、それに合わせますが、さしあたってなさそうなので、「ゼロ尤度関数」という名前にしてみました。

ゼロ尤度関数の特徴

確率密度関数は、μとσを固定値とする事で、定まる関数です。 L0は、確率密度関数とは違って、μとσは変数とする関数です。

L0で固定されているのは、データから求まる平均値（x-bar）や、標本分散の平方根（σ-bar）です。

例えば、平均値（x-bar）が0、標本分散の平方根（σ-bar）が1として、上のL0の式に入れると、下のようなグラフになります。

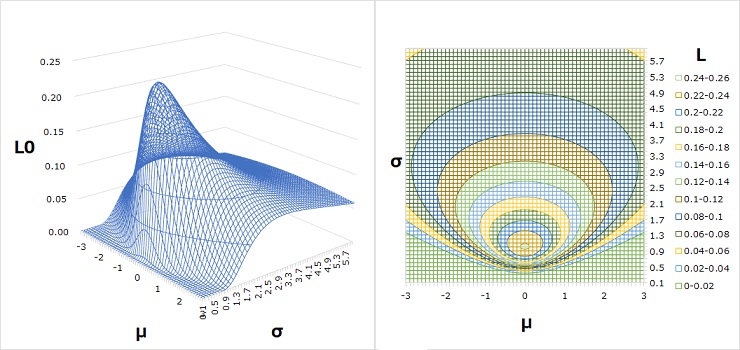
正規分布の尤度関数のサンプル数依存性のページに、標準正規分布になるデータの尤度関数について、サンプル数ごとに示していますが、それらよりも、丸みがある感じです。

平均値（x-bar）が0、標本分散の平方根（σ-bar）が1になる場合は、標準正規分布があります。

標準正規分布は、いろいろな時の基準として、応用に使われています。同様にして、上の例も、いろいろな応用を考える時の基準として使えそうです。

「標準正規ゼロ尤度関数」という名前にしてみました。