ベイズファクター

最近の文献では、尤度比分析として、ベイズファクター（ベイズ因子）が紹介されるようになって来ています。

ベイズファクターは、成り立ちがベイズ統計から来ていますが、そこから導かれた式は尤度比です。

尤度比検定との違い

尤度比検定とベイズファクターには、実質的な違いはないと、筆者は考えています。

ただ、これまでに先人が力を入れて研究して来たことは違っています。

このサイトでは、「尤度比検定を使うか？ベイズファクターを使うか？」ではなく、尤度比分析という分析方法として、両者の分野で培われて来たことを使うようスタンスです。和食にチーズを使ったり、洋食に味噌を使うような感じです。

以下の表は、これまでの傾向を整理したものです。

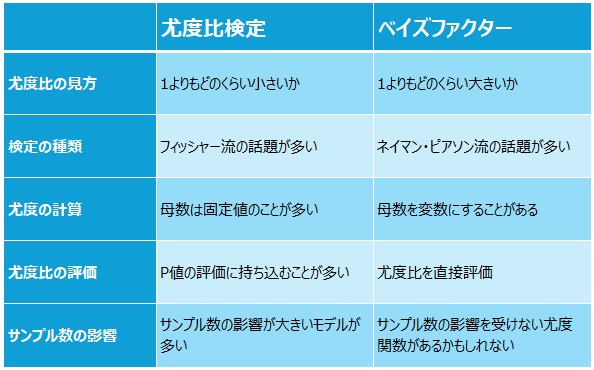
尤度比検定では、優れていると考えているモデルを分母にして、尤度比が１よりもどのくらい小さくなるのかを評価するのが一般的です。

ベイズファクターでは、優れていると考えているモデルを分子にして、尤度比が１よりもどのくらい大きくなるのかを評価するのが一般的です。

世の中の解説では、尤度比検定をフィッシャー流の検定として使う話題が多く、ベイズファクターをネイマン・ピアソン流の検定として使う話題が多いです。

ただ、これは活用の方向性が、今まで違っていたことが原因のようです。どちらかに限定されるものではないので、逆の使い方もできます。

ベイズ統計では、「母数が変数」という理論が整備されています。

ベイズファクターの解説では、「母数が変数」という考え方が当たり前のようにして使われる点が違います。また、「母数が変数」の理論によって、「ではない」の分布が使えるようになっています。

尤度比検定では、カイ二乗検定の形にして評価することが通例ですが、ベイズファクターでは、尤度比の大きさを直接評価することが通例です。

例えば、相関係数は、-1から1までの値しか取らないので、目安になる基準があります。一方、ベイズファクターの基準は、世の中にあるものの、相関係数のような根拠はないようです。

サンプル数への依存性は、尤度関数が正規分布の場合ですが、正規分布の場合、尤度比はサンプル数の影響を受けます。

そのため、正規分布の場合、尤度比は、P値がサンプル数の影響を大きく受けることの対策にはならないです。

効果量は、サンプル数の影響を受けない指標です。ベイズ統計では、尤度の計算がいろいろ研究されているので、尤度関数の作り方によっては、サンプル数の影響を受けない尤度比も作れるかもしれませんが、筆者には不明です。

「Rを使った〈全自動〉ベイズファクタ分析　js-STAR_XR+でかんたんベイズ仮説検定」　田中敏・中野博幸　著　北大路書房　2022
ベイズファクタについて、ソフトウェアの具体的な使い方も含めた解説書です。