２種類の対立仮説 のページで、フィッシャー流とネイマン・ピアソン流では、対立仮説の置き方が異なることを説明しています。
対立仮説の置き方が異なるので、分析の手順も異なっています。まとめると下の図になります。
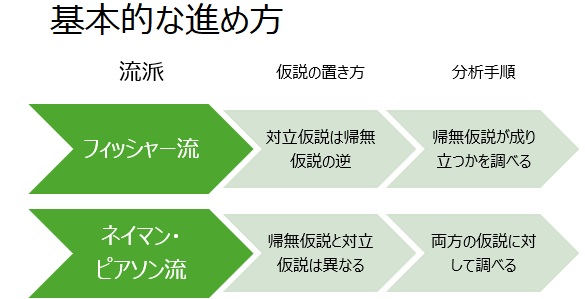
この関係を混同すると、議論がおかしな方向に進みがちです。 そのため、上の図の関係を正しく使うことは、とても大事です。
ところで、ややこしい話になるのですが、 仮説の置き方がフィッシャー流で、分析手順はネイマン・ピアソン流になっているにも関わらず、間違いではない場合があります。
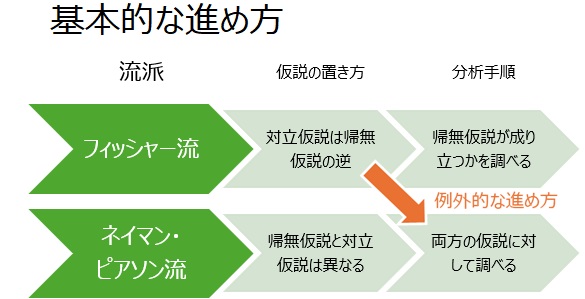
フィッシャー流の基本的な進め方では、「ではない」という対立仮説を作りますが、この仮説については具体的な分布を設定しません。 もしも、この対立仮説に対して具体的な分布を設定できるのなら、その場合はネイマン・ピアソン流の分析手順にしても、間違いにはならないです。
フィッシャー流として、帰無仮説を「平均値は0.5」、対立仮説を「平均値は0.5ではない」とした場合、帰無仮説の方については、例えば、平均値が0.5になる正規分布や二項分布を仮定できます。
この仮説に対して、分析手順をネイマン・ピアソン流にする場合は、「平均値は0.5ではない」という対立仮説を何らかの分布として設定する必要があります。 例えば、0.5というのが比率の場合は、比率は0から1までしかないので、「0から1までの一様分布」と置く方法があります。
このように「ではない」も分布にしてしまう方法は、 ベイズファクター の文献で見かけます。
コイン投げの場合、「平均値が0.5」というのは、「偏りはない」という意味です。 「平均値は0.5ではない」の対立仮説として、例えば「平均値が0.7」とする場合は、「面の出方に偏りはあるか」という検証の方法になります。
ところが、対立仮説を「0から1までの一様分布」とする場合は、「偏りはあるか」という話とは違って来ます。 「0から1までの一様分布」というのは、「投げる前に0から1の間で、発生確率がランダムに変動する」ということなので、これも「偏りはない」ということの一種です。 そのため、「面の出方に偏りはあるか」ということを検証をしたい場合には、「0から1までの一様分布」という設定は合わないです。
このように、「ではない」という仮説を表す分布は気を付けて使う必要があります。 「ではない」という仮説を、ネイマン・ピアソン流で扱う方法が開発されて来ていますが、今のところ、この方法が役に立つ事例に、筆者は出会ったことがないです。
順路
次は
第１種と第２種の誤り
