 �g�b�v�y�[�W |
�ЂƂ�̃y�[�W |
�ڎ��y�[�W |
���̃T�C�g�ɂ��� | ENGLISH
�g�b�v�y�[�W |
�ЂƂ�̃y�[�W |
�ڎ��y�[�W |
���̃T�C�g�ɂ��� | ENGLISH
 �g�b�v�y�[�W |
�ЂƂ�̃y�[�W |
�ڎ��y�[�W |
���̃T�C�g�ɂ��� | ENGLISH
�g�b�v�y�[�W |
�ЂƂ�̃y�[�W |
�ڎ��y�[�W |
���̃T�C�g�ɂ��� | ENGLISH
�������̎菇
��
�ۑ�B���̎菇
�̗v���v���ŁA
�f�[�^�T�C�G���X
�͏d�v�ȓ���ɂȂ�܂��B
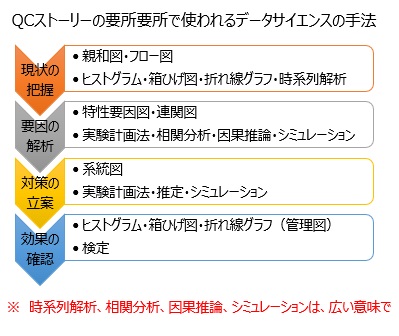
��ԏd�v�Ȏg�����́A������ʂ̑傫���A���ʊW�̋����A�Ƃ��������̂��ʓI�ɕ\�����邽�߂̕��@�Ƃ��Ăł��B
���̂ق��ɂ́A��������W�߂���A���ōl���������ł͎v���t���Ȃ�������������@�Ƃ��Ă��A�g�����Ƃ��ł��܂��B
�ȉ��́A �������̎菇 �ɉ����������ł����A �ۑ�B���̎菇 �ł��l�����͓����ł��B
�f�[�^�T�C�G���X�������ƁA�f�[�^�����ŕ����������ł���悤�ȋC���ɂȂ邱�Ƃ�����܂��B ���̋C�����́A�M�҂ɂ��悭�킩����̂ł����A ������f�[�^�����Ă��A�ǂ�Ȃɍ��x�ȕ��͕��@���g�����Ƃ��Ă��A���ꂾ���� ��������ۑ�B�� �ɂȂ��邱�Ƃ͂Ȃ��ł��B
�f�[�^�T�C�G���X�����ł͉������Ȃ����R�̂ЂƂ́A�����f�[�^�ɂ́A�u���Ă���v��A�u���ۂ��̂��̂�\���Ă��Ȃ��v�A�Ƃ������Ƃ��悭����_�ł��B ���̂悤�ȏł��A�u���̃f�[�^�ł̓_�����v�Ƃ͂��Ȃ��ŁA�����ɕK�v�ȏ����ł��邾�������o���K�v������܂��B ���߂Ĉ�������̃f�[�^�Ȃ�A�u���i�̌���͂ǂ̂悤�ɂȂ��Ă���̂��H�v�A�u���̃f�[�^�͉��̂��߂ɋL�^���Ă���̂��H�v�Ƃ��������Ƃ��A �f�[�^���痝�����邱�ƂŁA�����ɋߕt���܂��B
�f�[�^�T�C�G���X������Ă���ƁA �f�[�^�̕s���Ƃ��ẮA�u��������Ȃ��v�A�u������傫���v�A�u�ُ�l�⌇���l���������Ă���v�Ƃ������_���C�ɂȂ邩������܂���B �������A�����������_������̂ł����A�������ő�ςȂ̂́A�u���Ă���v��A�u���ۂ��̂��̂�\���Ă��Ȃ��v�Ƃ����_�ł��B �u���Ă���v��u���ۂ��̂��̂�\���Ă��Ȃ��v�́A�f�[�^�̔w�i�܂Ŕc�����Ă��Ȃ��Ƃ킩��Ȃ����Ƃ�����܂��B �I����āA���炭���Ă���C�t�����Ƃ�����܂��B
�u���Ă���v��A�u���ۂ��̂��̂�\���Ă��Ȃ��v�Ƃ����ł��A���������Ȃ�������Ȃ����́A��������悤�ɐi�߂܂��B
���̒��̉���ł́A���ۂ�\���f�[�^����A���̉���������悤�ȗႪ�A������������قƂ�ǂ�������܂���B
�Ƃ��낪���ۂ̖��ł́A����c���A�v����́A�����āA�Ƃ������i�K�ŁA�O�̒i�K�Ƃ͈Ⴄ�f�[�^�����ɍs�����Ƃ͒���������܂���B ���̂��߁A�ЂƂ̃f�[�^�Z�b�g�ƁA�����������@�Ŗ������ɂȂ���悤�Ȃ��Ƃɂ͂Ȃ�Ȃ��ł��B
�`���̌J��Ԃ��ɂȂ�̂ł����A ��������ۑ�B�� �Ƃ����ړI�ɑ��āA�f�[�^�T�C�G���X�͓���Ƃ��Ďg�����ƂɂȂ�܂��B �e�i�K�̂Ȃ���̕����́A�f�[�^�T�C�G���X�ł͂Ȃ��ł��B
�������Ɖۑ�B���̎菇 �̗v���v���Ńf�[�^�T�C�G���X���g���āA�����̖ړI�ɍs���������Ƃ�ڎw���܂��B
���̒��̃f�[�^�T�C�G���e�B�X�g�̃C���[�W�́A�uPython�����ӂȐl�v�A�u���x�̍������f��������l�v�Ƃ����������Œ蒅������悤�ł��B
�킸���ȃf�[�^���肪����ɂ��āA�f�[�^�ɂ��Ă̒m����o�����������Ė������������Ă����l���f�[�^�T�C�G���e�B�X�g�̂͂��ł����A���̂悤�ȃf�[�^�T�C�G���e�B�X�g�́A�ƂĂ����Ȃ��ł��B
�������Ɖۑ�B�� �̃y�[�W�ɃX�s�[�h���̘b������܂����A���ɖ������ł́A�Ƃɂ����X�s�[�h���厖�Ȏ�������܂��B
����c��������ʂ̊m�F�܂ł��A�u�P���Ԉȓ��v�A�u�������v�Ƃ������[���Ŏ��s����K�v�����邱�Ƃ�����܂��B ���������ꍇ�́A��ʓI�ȕ��͂��K�v�ȂƂ���ƁA��ʐ��̐��x���ǂ̒��x�K�v�Ȃ̂������ɂ߂āA�D�揇�ʂ����Ă����Ɨǂ��ł��B
�u�f�[�^�_�Ƃ����{���~���v�@�E�c�V�V���@���@�W�p�ЃC���^�[�i�V���i���@2020
�I�����_�́A������f�[�^�Ŋm�F���A��̌��ʂ��f�[�^�Ŋm�F���Ă����_�Ƃ��A���ɐi��ł邻���ł��B
�����Ō���f�[�^�́A���ʂȂǂ̌��ʌn�ł͂Ȃ��A���̗ʂȂǂ̌����n�ł��B
�������A���_�����l��A�J�^���O�̒l�ł͂Ȃ��A���������l�ł��B
�uIMPLEMENTING SIX SIGMA�v Forrest W. Breyfogle III�@���@WILEY�@2003
85%���炢���g���āADMAIC�̊e�i�K�Ŏg����@�ɂ��āA�̌n�I���ڍׂɐ������Ă��܂��B
�c��́A�Ɩ��̗���������e�[�}�ł���A���[����
��������̗��_
�̃e�[�}���V�b�N�X�V�O�}�̗���ōs���b��ADMADV�̘b�A�V�b�N�X�V�O�}�̉^�c�ɘb�ɂȂ��Ă��܂��B
��@�̊T���͉��L�ɂȂ�܂��B
D�F�ڋq�̐��̕���
M�F�T�O�̃O���t���A�W�̏��̃O���t���iQFD�i�i���@�\�W�J�j�j�A�f�[�^�̐��x�̕]��
A�F�����A�����A��A����
I�F�����v��@
C�F�Ǘ��}�A�M�����̕]��
�u�V�b�N�X�V�O�}�v Forrest W. Breyfogle III�@���@�O�c���O�@�Ė�@�G�R�m�~�X�g�Ё@2006
��̖{�̓��{��łł��B
���Ȃ݂ɁA�M�҂͓��{��ł͐}���قŃp���p���������x�ł��B
���̖{�͉p��̌������Ï��Ŕ����āA�ǂ�ł��܂��B�i�T���̂P���炢�̒l�i�ł����̂Łj
�uHead First�f�[�^��� : ���Ƃ��炾�Ŋo����f�[�^��͂̊�{�v�@Michael Milton ���@�勴�^�� �Ė�@�I���C���[�E�W���p���@2010
�f�[�^��͂̕��@�����łȂ��A�f�[�^��͂̋Ɩ����C���[�W���₷���悤�ɂȂ��Ă��܂��B
�@�f�[�^��͓���@�F�@��`�A�����A�]���A���f�̂S�i�K�Ńf�[�^��͂�i�߂�
�A�����@�F�@���_��������
�B�œK���@�F�@���v���ő�ɂ��邽�߂̎����̔z�������AExcel�̃\���o�[�ʼn���
�C�f�[�^�̉����@�F�������c���A���̑��̕ϐ��������ɂ����U�z�}���A��r�������Ώۖ��ɍ쐬����ƁA�Ⴂ���킩��
�D���������@�F�@���v�w�I�ȉ��������̘b�ł͂Ȃ��ł��B
�l�X�ȉ��������鎞�ɁA�u������������I�ԁv�ł͂Ȃ��A�u�����Ƃ����̏��Ȃ��������c���v�Ƃ����A�v���[�`������b�ɂȂ��Ă��܂��B
�E�x�C�Y���v�@�F�@�u�z���Ɣ��肳�ꂽ�ꍇ�ɁA�{���ɗz���ł���m���v���Z�o
�F��ϊm���@�F�@�m�M�x��\�����A���t�ł͂Ȃ��A���l�ŕ\���B�����̐l�̂��̐��l���O���t�ɂ���ƁA���̐��l�̊m���炵�����킩��
�G�o�����@�F�@���݂̑��ʂ̕ω������ۂɑ���̂͑�ςȂ̂ŁA��ʎs����S�~�����Ǝ҂ւ̃A���P�[�g����A�ω��̗L����
�H�q�X�g�O�����@�F�@�f�[�^�̏���ڂŔ��f
�I��A�@�F�@�Q�̕ϐ��̊W��
�J�덷�@�F�@�\���́A�덷�L����ƁA�u���ɂ��Ȃ������ҁv�A�u����Ȃ�m���v�A�u���D�ꂽ���f�v�ɂȂ���
�K�����[�V���i���f�[�^�x�[�X�@�F�@�f�[�^�̊W���Ǘ�����
�L�f�[�^�N���[�j���O�@�F�@Excel�ł̃f�[�^�̐����̎d���B�P�̃Z���ɕ����̃f�[�^���������Ă����Ԃ𐮌`���Ă����B
�����^�����̏��10�ʂ����̌�ɑ����̂ł����A10�Ԗڂ́A�u���Ȃ��̐��m���v�ł����B
�u�f�[�^��͂̎d�����A���ۂɂ���ė����l�̖{���I�v�A�Ǝv������e�ł����B
�u��ʕ��͂̋��ȏ��@�r�W�l�X�����͗{���u���v�@�O���[�r�X�@���@���m�o�ϐV��Ё@2016
���̖͂{�����A�u��r�v�Ƃ��Ă��܂��B
�_�O���t�́A�_�̒����Ŕ�r���܂����A�U�z�}�́A�c���Ɖ������r������̂Ƃ��Ă��܂��B
��r�����邱�ƂŁA���ʊW���킩��A���ʊW���킩��A����������������ɐi�߂���A�Ƃ��Ă��܂��B
�����v�l�����Ă���A�f�[�^���W�߂�B
��r�̎��́A�C���p�N�g�i�傫���j�A�M���b�v�i���فj�A�g�����h�i���ԓI�ȕω��j�A����i���z�j�A�p�^�[���i�@���j�̂T�B
��r�̋Z�p�́A�O���t�A���v�ʁA�����ɂ��\���i
�d��A����
�Ȃǁj�B
�t�F���~����F�������̑O��������āA��������Ɨʂ��v�Z������@�B
�u���������ł���!����Ƃ��Ẵf�[�^���p�p�v ���؋g��@���@�ĉj�Ё@2019
�v���Z�X���A
�E�ړI�E�����`����A
�E�w�W����肷��A�����c������A
�E�]������A
�E�v������肷��A
�E������l����
�Ƃ��Ă��܂��B
�u�f�[�^�̒��ɓ����͂Ȃ�����A�f�[�^�����n�߂邱�Ƃ͂�߂�v�A
�u�f�[�^���p�̑S�Ă�䖳���ɂ������́A��肪���m�ł͂Ȃ����ƂƁA���ƃf�[�^����v���Ă��Ȃ����Ɓv�A
�u�q�ϓI�ȕ]���̂��߂ɔ�r������v�A
�u����͗v���ɑ��Ă��Ȃ���ΈӖ����Ȃ��v�Ƃ����������̃��b�Z�[�W������܂����B
�u�u�������A��������肾������!�v���ǂ�ǂ��Ă���f�[�^�̓ǂݕ��E���������v ���؋g��@���@��a�o�Ł@2016
�ۑ�����̂T�̃v���Z�X�Ƃ��āA
�E�ۑ��`�A
�E����c���A
�E�ۑ�|�C���g����A
�E�v���̓���A
�E����̌����A
�Ƃ��Ă��܂��B
����ڕW���ǂ����������_����̂��̂Ȃ̂��m�ɂ��邱�Ƃ�A�ۑ����̓I�ɂ��邱�Ƃ��d������Ă��܂��B
���l�̊W�́A�U�z�}�⑊�W���Ŋm�F���Ă��܂��B
�{�S�̂́A�s�����̊ό��U���̊������ނɂ��Ă��܂��B
�u�������̂��߂̃f�[�^�����v �V�������@���@�N���X���f�B�A�E�p�u���b�V���O�@2019
���e�́A����̕��͂ł��B
�������̂S�̃v���Z�X���A
�E����̗����A
�E�����̌��ɂ߁A
�E�ł���̌���A
�E���s�A
�Ƃ��Ă��܂��B
�_���I�ȍl������������AExcel���g���ăf�[�^�̌X����������A�Ƃ����A�v���[�`�Ńf�[�^���͂�i�߂܂��B
�u���W�J���f�[�^�����@�X�s�[�f�B�[�Ɏ��v�ɂȂ���V��@�v�@�����Вm�Y�@���@���oBP�Ё@2015
������̂̃f�[�^�ŁA������̂̃c�[���ŁA�V���v���ɕ��͂���B
�f�[�^���Ȃ����͊��o�f�[�^�ŕ⋭����B
�������ׂ����͋t�Z�ōl����B
�萫�I�ȕ��͂́A��ʓI�ȕ��͂Ɠ������炢�厖�B
�萫�I�ȕ��͂Ƃ����̂́A�V�i���I���͂�VQC7����̎��B
��ʓI�ȕ��͂́A�f�[�^���g�����A�f�[�^���g������A�ǂ����Ă��ߋ��ɑ��Ă̕��͂����ł��Ȃ��B
�����̘b������ɂ́A�V�i���I���͂��d�v�B
�u�������̂��߂̃f�[�^���͊�b�u���v�@�����Вm�Y�@���@�r�W�l�X����o�ŎЁ@2020
�ǂ������鉻�́A���邱�Ƃōs���ɂȂ�����̂Ƃ��Ă��܂��B
�f�[�^���͂̃t���[�����[�N�Ƃ��āuPPDAC�T�C�N���v�Ƃ������̂��A�Љ��Ă��܂��B
�uPDCA�T�C�N���v�Ǝ��Ă��܂����APPDAC�́A
�EProblem�F�ۑ�̐ݒ�
�EPlan�F�����E���͂̌v��
�EData�F�����W
�EAnalysis�F���̐����E�W�v�E���́E�������f���\�z�Ȃ�
�EConclusion�F�Ƃ肠�����̌��_
�A�ƂȂ��Ă��܂��B
�u�܂��A�f�[�^�̂��Ƃ͍l�����Ƀr�W�l�X�ۑ�𒊏o�B
���ɁA���̒��Ńf�[�^���͂��K�v�ŁA��߂����A���ʂ̑傫�����̂�I�ԁv�Ƃ����菇�ɂȂ��Ă��܂��B
���̖{�̃f�[�^���͂ł́A�\�����f������邱�Ƃ��A�E�g�v�b�g�ɂȂ��Ă��܂��B
�u�������̂��߂̃f�[�^���͉��p�u���v�@�����Вm�Y�@���@�r�W�l�X����o�ŎЁ@2020
PPDAC�T�C�N���̏Љ�ȂǁA�ꕔ�̓��e�͏�L�̊�b�u���Əd�Ȃ��Ă��܂��B
���x�Ȑ������f�������낢��ƏЉ��Ă��܂����A�S�̓I�ɂ́AEXCEL�̉�A���͂��g����
�p�X���
�����āA�����̃f�[�^�͂�����e�ɂȂ��Ă��܂��B
�G�ߐ��̃��f�����Ȃǂ�����܂��B
���̖{�ɂ�����u���v��u�ۑ�v�́A�u��r���������Ɓv��u�����ŕ\�������ϐ��̊W�v�Ƃ����������̈Ӗ��Ŏg���Ă��܂��B
�u�A���S���Y���v�l�p�@�������̍ŋ��c�[���v�@�u���C�A���E�N���X�`�����A�g���E�O���t�B�X�@���@���쏑�[�@2017
�R���s���[�^�����̂��߂ɍl�Ă���Ă����A���S���Y�����A���퐶���ɂ����p���悤�Ƃ��Ă���{�ł��B
�����Ă���A���S���Y���́A�œK��~�A�T���A�\�[�g�A�L���V���A�X�P�W���[�����O�A
�x�C�Y�̖@��
�A
�I�[�o�[�t�B�b�e�B���O
�A�ɘa�@�A�����_�����A
�l�b�g���[�L���O
�A
�Q�[�����_
�ł��B
�S�ʓI�ɁA����ꂽ���ԂƏ��̒��ŁA�x�X�g�Ǝv����s�������邽�߂̘b�����Ă��銴���ł����B
�u���n�̂��߂̗��n�I�������@Excel�Ŏ��H���鐔���I�E���v�I���̓A�v���[�`�v�@���c���@���@�I�[���Ё@2008
��A����
�Ȃǂ̓��v�I�ȕ��@��A
�������g�����V�~�����[�V�����A�����v��@�Ȃǂ��Љ�Ă��܂��B
�u�Љ�E����̓��v�̌����Ɗ��p�@�f�[�^�ɂ��������v�@�v�ې^�l�@�ҁ@���q���X�@2015
��A����
��
���q����
���g���������̌��̎d����A�f�[�^�̊W�̌������Љ�Ă��܂��B
�u���E�ōł��������������@�@���������邽�߂̍s���o�ϊw�A���������f���邽�߂̓��v�w�v�@���`���[�h�EE.�j�X�x�b�g�@���@�y�Ё@2018
���Ȃ�f��I�ɁA�u�����������̍l�����v��������Ă��܂��B
���@�_��
�s���o�ϊw
�ɂ��l�Ԃ̍s���̃N�Z�̒m�����Q�l�ɂ��A
���ʐ��_
�W�̓��v�w�ƁA
�_���w
���g���āA�q�ϓI�ɕ�������������b������܂��B
���H


 ����
����c���̂��߂̃f�[�^�T�C�G���X
����
����c���̂��߂̃f�[�^�T�C�G���X

