１次元散布図 と ２次元散布図 の大きな違いは、２次元散布図は、単に分布を見るという事だけではなく、 ２つの次元（２つの変数）の関係を見る目的でも使われることと思います。 広い意味での 相関性 を見るために使います。
ネットワークグラフ の場合は、分布は見えませんが、たくさんの物の関係を見ることができます。
２次元分布のグラフや関係のグラフは、 多変量解析 、 データマイニング 、 機械学習 などを進めたい時に、頼りになるグラフです。
２次元散布図やネットワークグラフは、 変数の類似度の分析 、 カテゴリの類似度の分析 、 サンプルの類似度の分析 の中で、分析結果を見る方法として使うことがあります。
お互いの長所と短所を考えて使い分けます。
ネットワークグラフは、「完全に類似・一部が類似・完全に類似しない」や「関係が強い・関係が弱い・関係がまったくない」といったことを表現できます。
例えば、下図の
隣接行列
のデータでネットワークグラフを作ると右図になります。
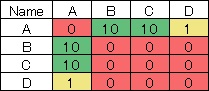
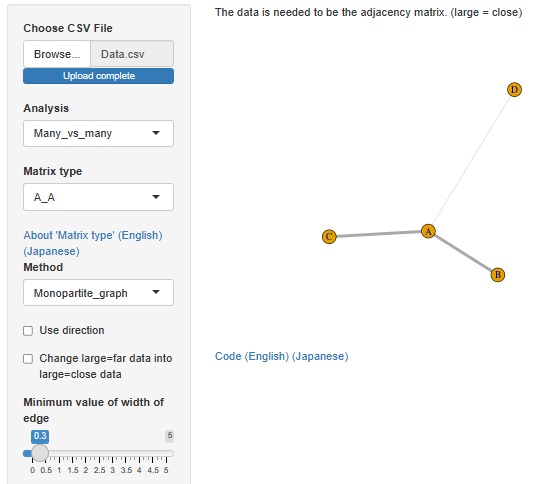
隣接行列の数字がエッジ（線）の有無や、太さの違いとしてそのまま表現されています。
このデータを距離（大きい＝遠い）のデータに変換して、
多次元尺度構成法
を使って、散布図にすると下図になります。
ネットワークグラフで、エッジが消えたような図ができます。
Dから見た時の、A、B、Cが同じようになっていて、違いが見えません。
また、A、B、Cがひとつのグループに見えますが、BとCにはエッジがないことがわからなくなっています。
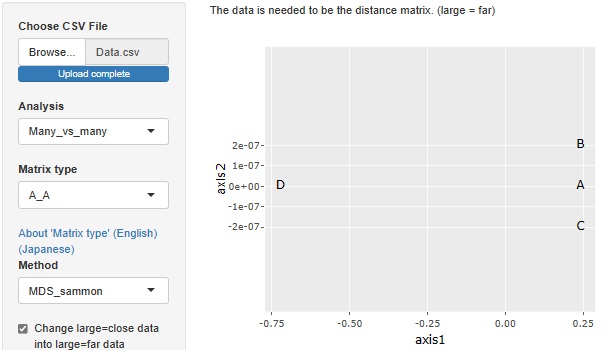
また、エッジに向きの情報を付けたい時には、散布図ではできません。
ネットワークグラフは、エッジ（線）があるので、グラフがごちゃごちゃしやすいです。 また、数十個くらいの関係を表す時は良いのですが、それ以上の規模になると、コンピュータの処理が大変になりやすいです。
２次元散布図には、ネットワークグラフでは処理が厳しい時に、表現しきれていないことがあるのを承知の上で、 分析する使い方があります。
分析対象によるのですが、例えば、扱っているものが「位置」だったら、AとB、AとCが近い場合、「BとCがすごく遠い」ということはあり得ません。 そのため、分析対象によっては、ネットワークグラフを使うことには意味がなく、散布図の方が同じことをすっきり表現できることがあります。
順路
次は
２次元散布図
