点過程は、ある瞬間(点)のことを表しているデータでできています。 時系列解析 の一種です。
点過程として、ここでは3タイプに分けました。 グラフにすると似ていますが、含まれている情報が違います。 下記の例は、「日」を単位としていますが、もっと細かくしたとしても、同様です。
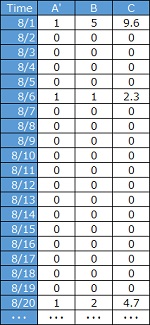
点過程のデータは、タイミングと大きさを表すデータの場合が多いので、下のグラフは棒グラフにしています。 ちなみに、他の 時系列解析 では、折れ線グラフの方が良いことが多いです。
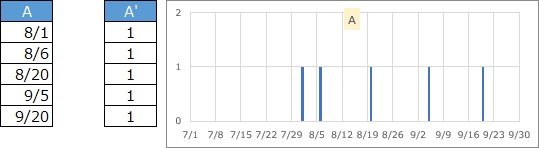
イベントが発生した日だけのデータの場合です。地震のデータなら、発生したかどうかだけがわかります。
グラフは、「1」という列を追加すると作れます。

値が整数で、ひとつのデータは1以外の整数の場合もあって、その日の件数を表します。 Aタイプを集計すると、このタイプにすることができます。 また、細かな時間で記録を残すと、Bタイプではなく、Aタイプのデータを作れます。
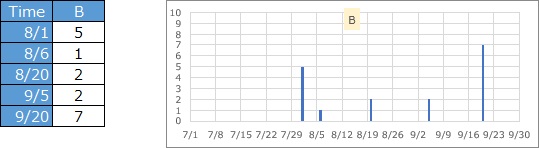
ひとつのデータが表す件数は1件ですが、値の大きさを表しています。地震のデータなら、マグニチュードや震度がこれに相当します。
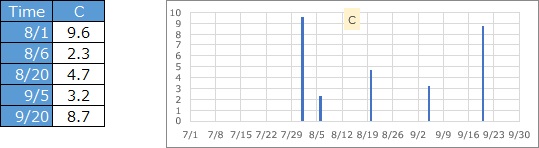
上記のAタイプで、下のようなデータがあったとします。
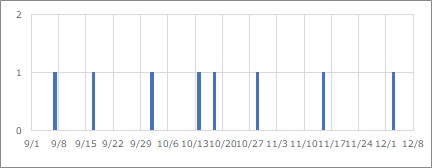
発生率は、だいたい一定のように見えますが、それをもっとはっきり見るには、下のように時刻の差を計算して、散布図を作ります。
時間解析になります。
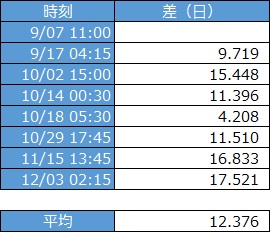
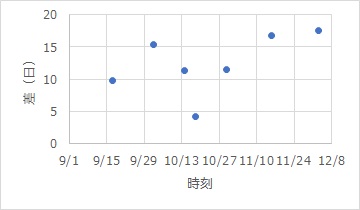
ポアソン過程は、発生率が一定(定常的)であることを仮定しますので、「一定」と仮定しても良さそうかどうかの検討をする時にも、この分析方法は便利です。
発生件数の累積を計算して、散布図にする方法もあります。
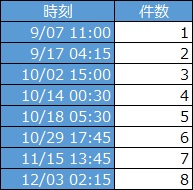
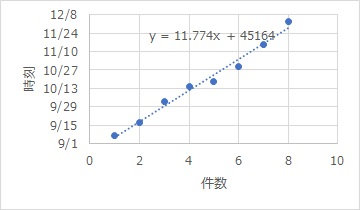
時刻をX軸、件数をY軸ではなく、ここでは、時刻をY軸、件数をX軸にしています。 こうすると、各件数に対して、時刻にばらつきがあるモデルとして、単回帰分析ができます。 (回帰分析への測定誤差の影響を参照)
ほぼ一直線に並んでいれば、発生率が一定と考えられます。
時間解析では、時間の平均値として「12.376」、回帰分析では傾きとして「11.774」という数字が求まっていますが、これはいずれも単位が「日/件」です。 約12日に1件発生していることがわかります。
計算方法が異なるので、ぴったり同じにはなりませんが、2つの方法でだいたい同じ数字が求まります。
ちなみに、これらの逆数は、0.083(= 1/12)ですが、これは単位が「件/日」で1日あたりの発生確率として使える数字になります。
点過程には、ポアソン過程など、数学的な研究が進んでいます。 こうした理論は点過程のデータだけを対象としているのですが、それもあり、「なぜ、このタイミングで起きた?」という疑問の解決には向いていないです。
点過程の数学的な理論のような美しさはないですが、「なぜ」にアプローチするには、下記のようなアプローチの方が向いています。
点過程のデータは、データがない時を補えば、 自己相関分析 や スペクトル解析 で使うようなデータの間隔が、一定時間にすることができます。 こうすることで、 時系列解析 の他のタイプのアプローチもできます。
Aタイプにこの変換をすると、
0-1データ
になります。
準周期データの分析 で、 3次データ(ラベル付きデータ)の解析 の段階で前処理をされたセンサーデータと紐付けることで、点過程の原因に切り込む方法があります。
また、 逆時間集計 で、時間をさかのぼる時の基点として、点過程データの時刻を使う方法もあります。
「イベント時系列解析入門」 小山慎介・島崎秀昭 著 近代科学社 2023
点過程の専門書です。イベント1回ずつの発生時刻のデータがある場合と、等間隔の時間のそれぞれの範囲のイベント発生回数がある場合、状態空間モデルがあります。
リニューアル過程:イベント生成率が直前のイベント生成時刻に依存する。
イベント間隔分布として、ガンマ分布、ワイブル分布、逆ガウス分布。
「非線形時系列解析の基礎理論」 平田祥人・陳洛南・合原一幸 著 東京大学出版会 2023
点過程の分析方法として、
窓
を動かして集計していく方法を紹介しています。
この方法は、点過程ではない時系列データでも使えます。
「Machine Learning実践の極意 機械学習システム構築の勘所をつかむ!」 Henrik Brink 他 著 インプレス 2017
時系列データは、データの時間間隔が一定のものと、イベントが発生した時だけのもの(点過程)の2種類。
解析の方法には、それらの組み合わせも。
「現場ですぐ使える時系列データ分析 データサイエンティストのための基礎知識」 横内大介・青木義充 著 技術評論社 2014
時系列データと、点過程データの違いの説明から始まります。
時系列データは、値の変化のデータです。折れ線グラフが一般的です。
一方、点過程データは、値の発生のタイミングと、その時の大きさを表します。
こちらは、横軸を時刻にした
棒グラフ
にします。
「時系列解析の方法」 尾崎統・北川源四郎 編 朝倉書店 1998
点過程モデルは、時間軸上に発生時刻を示す点が置かれている確率現象。
ここでは、地震発生の解析をしている。
「空間データモデリング 空間統計学の応用」 間瀬茂・武田純 著 共立出版 2001
統計物理のギブス点過程が、画像処理の理論に使われています。
「統計学をめぐる散歩道 ツキは続く?続かない?」 石黒真木夫 著 岩波書店 2020
点過程の章があります。
地震の予報は、地下が観測できないために天気予報のように細かくできず、数十年の間に1回起きる確率というように、長い期間が対象になることを説明しています。
「ガウス過程と機械学習」 持橋大地・大羽成征 著 講談社 2019
点の発生率が一定とするポアソン過程では、不十分として、これを時間の関数とする、Cox過程を紹介しています、
「確率論の基礎と発展」 飛田武幸 著 共立出版 2011
確率過程について数学的な扱い方を詳しく書いていて、その中でポアソン過程が出て来ます。
「空間統計学 自然科学から人文・社会科学まで」 瀬谷創・堤盛人 著 朝倉書店 2014
空間データには、格子状のデータと点過程のデータがあるものの、この本では点過程の方は扱っていないと書かれています。
点過程については、「空間データモデリング 間瀬茂・武田純 著」を紹介しています。
順路


 次は
ポアソン過程
次は
ポアソン過程

