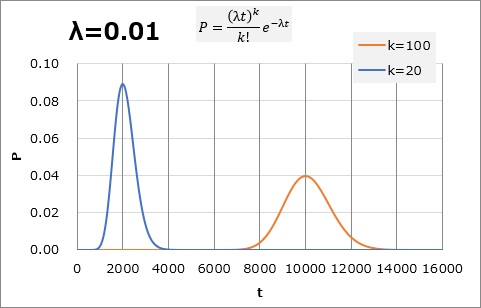
点過程のデータの発生の仕方をポアソン分布とみなした場合、つまり、「等確率でランダムに発生する」、とみなした場合、ポアソン過程と呼ばれています。
平均で、100時間で1件の割合(0.01)で発生する場合、20件発生には2000時間、100件発生には10000時間かかることは想像できますが、その件数の到達までの時間には、ある程度の幅があることも想像できます。 その幅をポアソン分布で仮定すると下のグラフのようになります。
100件到達が8000時間だと「早過ぎるのでは?」、12000時間だと「遅過ぎるのでは?」と思いたくなるかもしれませんが、
それくらいは、「100時間で1件」という仮定では、ばらつきの範囲で、特に異常ではないことがわかります。

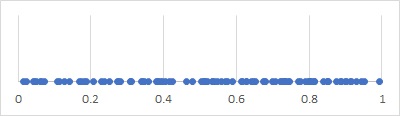
上のように、ポアソン過程になっているデータがあったとします。データは100個あります。間隔がランダムです。
時刻の差を計算して、間隔のデータを作り、ヒストグラムにすると、指数分布になっている様子がわかります。
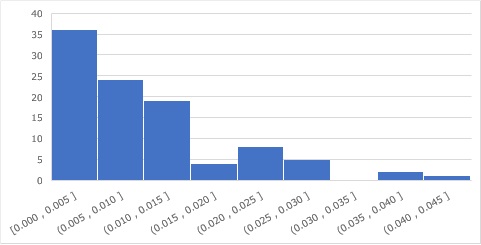
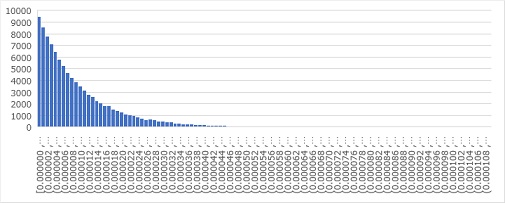
ちなみに、「いびつだから、指数分布ではないのでは?」という疑問の解消のために、100000個のデータで同様の作業をすると、下のグラフになります。
このくらいデータがあると、発生がランダムだからといって、ランダムな分布になるのではなく、きれいな分布になる様子がわかります。
ポアソン過程では、発生確率が一定、という仮定があります。 この仮定の確認方法は、 点過程分析のページにあります。
「イベント時系列解析入門」 小山慎介・島崎秀昭 著 近代科学社 2023
点過程の専門書です。
「ガウス過程と機械学習」 持橋大地・大羽成征 著 講談社 2019
点の発生率が一定とするポアソン点過程では、不十分として、これを時間の関数とする、Cox過程を紹介しています、
「確率論の基礎と発展」 飛田武幸 著 共立出版 2011
確率過程について数学的な扱い方を詳しく書いていて、その中でポアソン過程が出て来ます。
「確率思考の戦略論 USJでも実証された数学マーケティングの力」 森岡毅・今西聖貴 著 KADOKAWA 2016
マーケティング・サイエンスの本です。
顧客がランダムに発生するというポアソン過程の話から、さらに進んだ確率モデルが出て来ます。
順路


 次は
環境と品質
次は
環境と品質

