非対称な因果の因果推論

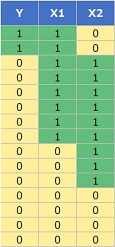
このページで扱う「非対称な因果」ですが、例としては、下のようなデータです。 Yが結果を表す変数で、X1とX2が原因を表す変数と仮定しています。

Yが1になる場合が、X1が1で、X2が0の場合と決まっています。しかし、Yが0になる場合は、色々な条件があります。このページでは、これを「非対称」と呼んでいます。
QCA

なお、質的比較分析（QCA）の解説で、ある事象が起きる条件の反対が、ある事象が起きない条件になっていない時を「非対称」と呼んでいるものがあります。このページの内容と似ています。

原因系が２変数以上（２因子以上）の時に、こういうことが起きます。まれに起きることの、起き方のひとつです。

このような場合、例えば、X1とYだけを見ると、「X1とYは関係がない。」となります。そのため、原因の変数が１つの場合よりも、発見が難しいです。

原因の変数が２つ以上の場合を見つける方法

サンプル数によって、適した方法が違って来ます。

サンプル数が多い時の方法は、確率の大小を調べられるので、相反する事例が混ざっていたとしても、調べられます。ただ、サンプル数が少ない事例は、「統計的に意味がなさそう」と判断されることがあるので、サンプル数が少ないデータには向きません。

サンプル数が少ない時の方法は、違いがはっきり出ている場合には使いやすいです。はっきりしていない場合は、最初の仮説として使う感じが良いかと思います。仮説を最初に置いて、サンプル数を増やして確認する進め方になります。

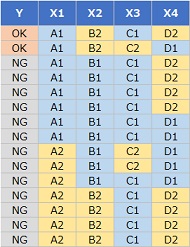
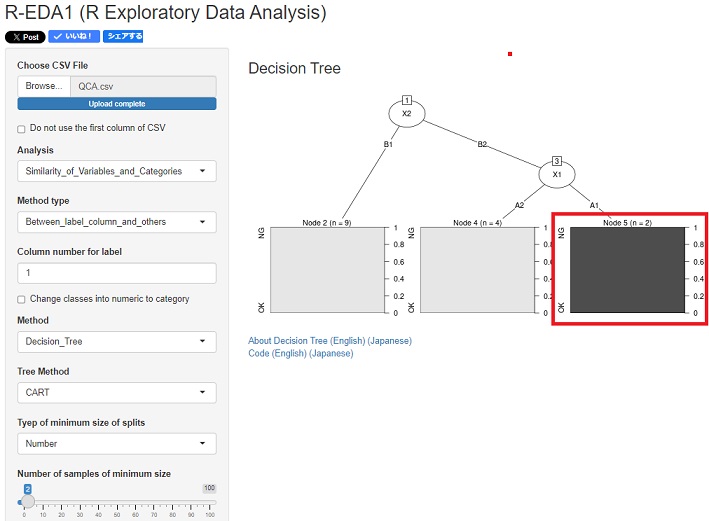
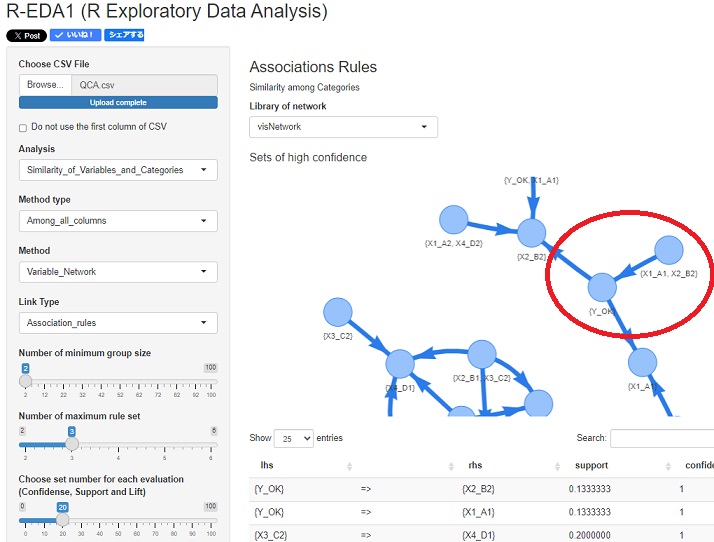
下の例は、 R-EDA1 の決定木とアソシエーション分析を使った例です。左がデータ、右が分析結果です。 X1がA1、X2がB2という条件だと、YがOKになっていることが分離できています。
QCA QCA QCA

このページの例のように、Yが0と1の2値の場合は、ロジスティック回帰分析でも分析できます。

Yは量的データの場合は、一般的な回帰分析系の方法になりますが、各変数の効果を足し合わせるモデルなので合わないです。交互作用項を工夫する方法はありますが、結果の考察が難しいです。

過程追跡は、このページのようなデータよりもさらに事例が少なく、１回しか起きたことがないような場合の方法です。