一口に「データ」と言っても、いろいろあります。
まず、パッと見てわかる違いがあります。
量的と質的や、連続と離散などです。
さらには、データの性質の違いもあります。
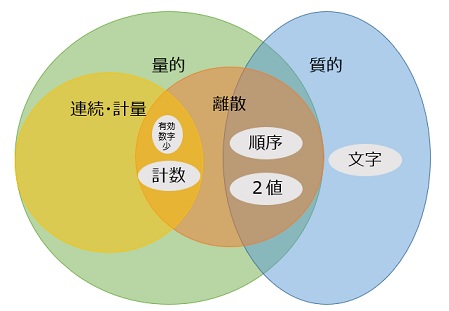
量的データは、「1,2,3」等の数値で表されるデータです。
質的データは、「A,B,C」等の文字で表されるデータです。 数値で表されていても、１番地、２番地などのように、数値の大きさに意味がない時は、質的データとして扱います。
データサイエンス の使い方として、質的データと量的データの区別はしても、量的データは全部同じようにモデルにいれる場合があります。 例えば、データの意味を詳しく知らないデータセットに対して、重回帰分析を適用する場合です。 ただ、そのアプローチだと、うまく行かない時に、非線形の複雑なモデルを使うような方向性しかないです。
量的データの区別をすると、 数理モデリング によるアプローチを進める時の参考になります。
連続データと離散データは、どちらも量的データです。
連続データは、温度などのように、原理的には、ほぼ無限に細かい値があるデータです。
離散データは、飛び飛びの数値しかないデータです。 整数値しかないようなデータが代表的です。
なお、 有効数字 が少ないと、連続データだとしても、見た目は離散的になります。 例えば、１刻みのデータを連続データと考えるか、離散データと考えるかは、場合によって使い分けます。
計量データと計数データは、どちらも量的データです。
計量データは、連続データとほぼ同じ意味です。
計数データは、人数や頻度のように、０以上の整数しか存在しないデータです。 この場合は、離散データの一種です。
このような、計数データを計数データで割ると「比率」が計算できますが、比率は計数データです。 比率の数理は、計数データの数理を使います。 離散的か連続的かというデータの見た目だけだと、計数データかどうかの判断は難しいです。
量的データの中でも、長さ、重さ、エネルギー、比率、などは大きさを表しています。
位置データというのは、座標のように日常的な意味での位置だけでなく、温度なども表します。
ちなみに、例えば、エネルギーと温度には関係式があるように、大きさデータと位置データは完全に別のものではないです。
スカラーとベクトルは、物理学でよく出て来るデータの見方です。
スカラーは、上記の大きさデータと同じものです。 ベクトルは、大きさと向きを持つもので、例えば、速度や力があります。
「可加算データ」、「非加算データ」では筆者の造語です。 可加算データは、足し合わせる（加算）ができる（可）データなことで、非加算データは、加算できないデータのことです。
大きさデータの中で、長さや重さは、可加算です。 比率データは、可加算と非加算の両方があり、分子と分母の内容で変わります。
位置データは、非加算です。
可加算データは、 測度論 の中で、数学的な研究が進んでいます。
質的データは、「出現回数を数える」といった集計が初歩的な扱い方です。 量的データ（離散データ）のようにして扱うことで応用が広がります。
例えば、マラソンをすると、 １、２、３、４といった、順番のデータができますが、順番の間のタイムは、ばらばらです。 順序データには、このような特徴があります。
順序データは教科書では質的データとして分類されますが、 順番の間隔には意味のないことを考慮すれば、量的なデータとして扱うこともできます。
２値データは、質的データの一種です。
「あり・なし」、「真・偽」、「OK、NG」、「良品、不良品」、「表、裏」などのように、２つの値しかないデータです。
２値データは、論理的に扱いやすいので、プログラミングでいろいろな処理をしやすいです。 また、それぞれを「０」と「１」に変換すると、数値として処理できるようになります。 数量化理論 や 0-1データの時系列解析 など、様々な手法があります。
パターン認識 では、「−１」と「１」に変換して、「０より大きいかどうかで、どちらかを判定」という使い方をすることもあります。
順路
次は
誤差
