測度論を確率論の基礎として説明している書籍が、いくつかあります。 確率論は、統計学の基礎なので、測度論は統計学の基礎ということにもなります。
測度論や、測度論的確率論が学問の世界で広く支持され、活用されています。 学問の世界としては、既に完成しているものとして語られるのが普通のようです。 ただ、筆者としては、現実のデータの話では、それだけではないような気がしています。 このページは、未整理のアイディアも書いています。 筆者の理解不足や、誤解によるものがあるとは思います。必要に応じて、加筆・修正する方針で、このページは書いています。
測度論は、数学の一分野で、文字通り「測度」を説明しています。
測度は、日常的には、「量」と呼ばれているものの一種です。 「量」と呼ばれているもの中でも、長さ、面積、重さのように足し算ができるものが、測度の定義に当てはまって来るようです。
測度論では、「測度とは・・・」と、辞書のように話し言葉だけで説明するのではなく、数学の言葉で説明します。 数学の言葉で表現できると、性質や特徴について、数学的な研究ができるようになります。
「２つのグループの重なる部分と、重ならない部分」、「全体と一部」といった考え方を扱う数学の分野に「集合論」があります。
測度論では、「測度」を集合論を使って定義します。
測度論では、測度を集合論を使って定義する時に、「測る物」と「測られる物」に分けることで、「測る」ということの定義をしています。
順番としては、まず、測られる物の性質を集合論を使って定義します。 次に、それに対応する形で、測る物を定義します。
「確率の説明をするのに、集合論を使うのは、よくある話。しかし、長さの話をするのに、なぜ、集合論を使うのか？」というのは、筆者がよくわからないところでした。
長さとして得ているものは、部分の足し合わせであり、「全体は、部分の集まり」、「足し合わせる時に重なる部分はない」ということを表現するのに、 集合論の書き方がちょうど良いというのが理由のようです。
測度論では、量の中でも、長さや面積について説明するのが普通です。 確率論の話もする場合は、「確率」も量の一種と考えて、確率を扱っています。
世の中には、重さ、明るさ、等々、量にはいろいろなものがありますが、そういったいろいろな量を扱っている測度論の解説を、 筆者は見た事がありません。
データの見分け・使い分け のページにありますが、測度論が扱っている量は、「量的データ」や「量的変数」と言われて データサイエンス の中で出て来るものの、一部です。
測度論の立場では、確率は、測度の一種です。 全部足すと１になる測度が、確率という測度の定義になっています。 そのため、測度論の立場では、確率論は確率という測度の性質を扱う学問ということになります。
「確率の説明をするのに、集合論を使うのは、よくある話。」と上で書きましたが、「確率とは何か？」を説明するのに、集合論は便利です。 「確率として扱っている事象は、全体の一部」という説明は、集合論そのものです。
そのため、確率と集合のつながり方は、２つあるようです。 ひとつは、測度論経由で、確率が測度の一種だから、というつながりです。測度の説明に集合が使われます。
もうひとつは、確率は、もともと集合の全体と部分の関係を表す量、というつながりです。確率の説明に、直接、集合が使われます。
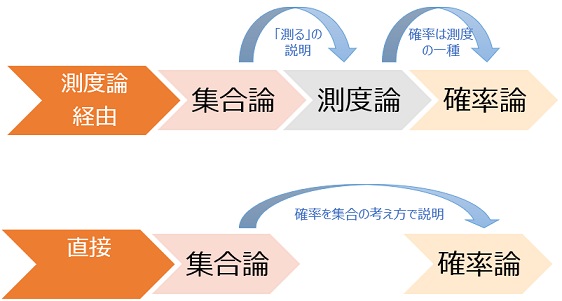
測度論の立場だと、測度論を経由しない方の確率論は、経由する方に含まれそうですが、そうではないような気もしています。 何か例があるのかもしれませんが、筆者は思い当たらないでいます。
集合論から出て来る確率論を２つ書きましたが、もうひとつあるような気がしています。 集合論だと、全体の集合は何か決まった性質があって、しかもそれが全体にわたって一様であることを前提としています。
現実の世界で、人が確率を思い浮かべる時は、全体の集合はあっても、一様ではないことを前提にしているようなところがポイントになりそうです。
数学の授業では、確率と積分は別の分野のようにして学びますが、測度論的確率論では一緒になっています。
まず、確率は足して１になるものなので、「足す」という操作を高度にする時に積分が出て来ます。
また、平均値のような統計量は、期待値の一種として計算するのですが、期待値の計算は、すべての確率について足し合わせたものなので、この計算でも積分が出て来ます。
空間の見方は、長さ、面積、体積という順に拡張できます。 確率の場合は、面積に近い性質を持っていますが、空間の中の面積のように、縦と横の単位が同じものではないところが違っています。
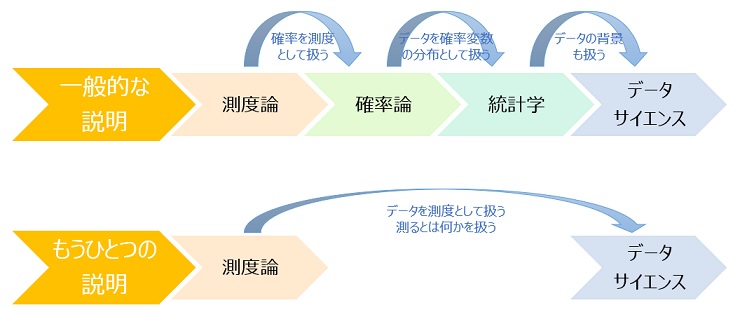
「測度論は、確率論の基礎。 確率論は、統計学の基礎。 統計学は、データサイエンスの基礎。だから、測度論は、データサイエンスの基礎」というのが、一般的な説明と言って良いようです。
筆者としては、 「測度論は、『測る』とはどういう事なのかを扱う。これはデータとは何かを扱っていることになる。だから、測度論は、データサイエンスの基礎」という説明もあると思います。 この関係を考える時は、確率の話は入っていないです。
どちらかが正しいという訳ではなく、２つの考え方があると思います。
例えば、「1.5mm」というデータがあった時に、前者の見方だと、「確率的に得られたもの」です。
後者の見方だと、「測って得られたもの」です。
確率論は、測度論を取り入れることで、様々な研究がされています。 ただ、そうした研究は、数学としての興味で進められているようで、データサイエンスが扱っているようなテーマに対して、役に立つようなものではない感じです。
データの見分け・使い分け のページに、量的データの区別として、「大きさデータと位置データ」、「可加算データと非加算データ」を書いています。 この区別は「測度論の測度に当てはまるか？」ということにもなります。
データの見分け・使い分け のページに少し詳しく書きましたが、この区別をすると、データサイエンスの応用が広がります。
測度論は、「測る」ということを扱う学問ですが、「測る」という行為を扱っている訳ではないです。 長さや面積のような量について、 「測るもの」、「測られるもの」の数学的な定義を扱っています。
「測る」という行為は、計測工学になって来ますが、例えば、長さだと、「これが1mm」という基準を決めます。 「測る」というのは、その基準に対して、測りたいものの大きさを調べます。 測る時に、物理法則や 回帰分析 を使うことがあり、そういう時は数学が活用されますが、測度論を使う訳ではないです。
測度論は具体的な量の大きさを得ることを目的としていないので、「基準に対してどうなのか？」といった考え方は出てこないです。
測定のページにある計測工学の本は、身近な量を扱っています。測度論は出て来ません。 測度論は、「長さ」を研究してきた学問ですが、 長さを測る時だとしても、測度論は出て来ません。
ただ、「実際に何かを測る時に測度論は不要」というと、そうは言い切れないようです。
素粒子や宇宙の世界など、身近ではない物を扱う世界では、測れるもの、測りたいものを研究するところからになるので、測度論が大いに関係して来るようです。
ルベーグ積分は、いわゆる積分の一種です。
高校で教わる積分は、リーマン積分と呼ばれるもので、ルベーグ積分はそれをさらにパワーアップさせたものです。 リーマン積分では積分できないけれども、ルベーグ積分では扱える例として、ディリクレ関数があります。
測度と積分は切っても切れない関係です。 測度が定義できていないと、積分の定義ができませんし、測度自体が「足し合わせる」という、積分の考え方でできています。
測度は、積分を再考する中で生まれて来たもののようです。
確率論の世界では、積分がよく出て来ます。平均値など、期待値の計算が積分なためです。
話は変わりますが、測度とルベーグ積分は一緒に研究されて来たものなので、 確率は測度の一種として考えていくのなら、「確率を扱うのにルベーグ積分は適している」、ということになります。
では、現実に起こっているような現象に確率の考え方を使ってアプローチをする時に、リーマン積分ではだめで、ルベーグ積分を知らないといけないのかというと、 そういうことはないようです。 ルベーグ積分の解説書だと、高度な関数の積分が出て来ますが、確率論で出て来る積分は、それほど高度ではないです。
上記の「データの取得における測度論の活用」と似ていて、身近ではない物を扱う世界の積分では、ルベーグ積分が大いに役に立つ場面があるのかもしれませんが、 社会の中や、会社の中ではないような気がします。
「測度の考え方 測り測られることの数学 人間が持っていた直観と確信が息づく数学」 原啓介 著 技術評論社 2023
測度の本では、測度の定義から始めるものが多いですが、この本は、そのような定義が出て来る背景から、丁寧に説明されています。
測度について、「測るとはどういうことか」、から始まり、集合や実数などの、数学的な道具の説明を丁寧に進めてからになっています。
測度論とは、「2cmは、1cmが2個」といったように、測るということは、小さなものの合計になっていて、その小さなものは、どこまでも小さくできるということを、
数学的に厳密に説明するものと言えるようです。
「量の測度」 アンリ・ルベーグ 著 みすず書房 2016（初版は1976）
数、面積、体積、測定可能な量と続き、最後の章がそれらを扱うための、微分法・積分法となっています。
これらは学校教育の中で教えられるものですが、著者は、この本で著者による説明を展開しています。
第６章で、「増加と減少を許すものはすべて量」という古い定義から、「驚き」や「国家予算」といった様々な量に想いを巡らせますが、
著者が「量」と考えているものは、量の公理を満たすものとしています。
著者の考え方だと、質量は量ですが、温度は量ではないです。温度の場合は、30℃と40℃を足しても、70℃にはならないですが、
このように足し算ができるものと、できないもので分けています。
「無限をつつみこむ量 ルベーグの独創」 志賀浩二 著 紀伊國屋書店 2008
測度やルベーグ積分が作られた歴史的な流れを、無限という概念がどのように取り込まれたのか、ということを踏まえて説明しています。
「工学者のためのルベーグ積分と関数空間入門」 篠崎寿夫・松浦武信 著 現代工学社 1991
ベクトル空間、ヒルベルト空間、超関数のフーリエ変換といった分野でルベーグ積分を使うための入門書になっています。
「物理・工学のためのルベーグ積分入門」 G.テンプル 著 ダイヤモンド社 1981
ルベーグ積分を丁寧に解説している本ですが、数学者にとっては易しい書き方をしている感じです。
「ルベーグ積分 理論と計算方法」 岩田耕一郎 著 森北出版 2015
定理と証明がたくさん紹介されていて、最後の方でフーリエ変換につながっています。
「応用のための確率論入門」 中塚利直 著 岩波書店 2010
確率測度、つまり、測度としてきちんと定義された確率を使って、分布や定常性といった性質を解説しています。
測度論の前に集合論。確率論につなげるために重要なのは、有限、可算無限、連続の濃度、連続の濃度より大きい濃度の区別。
確率論で出て来る積分は、ほとんどがルベーグ積分。
「測度・確率・ルベーグ積分」 原啓介 著 講談社 2017
19世紀の確率論の中には、奇妙な問題が見られるが、20世紀に入って測度論を使った確率論が整備される前だからとしています。
「長さとは」、「測るとは」といったことが、数学的な定義がない状態で、「長さ」や「測る」ということに関する確率的な議論をしていたのが、
19世紀に起きた混乱の原因だったようです。
確率論は、有限測度の測度論だが、確率論独特の問題意識があるところが違っている。
その代表的なものが、確率の独立性。
「統計学への確率論,その先へ ゼロからの測度論的理解と漸近理論への架け橋」 清水泰隆 著 内田老鶴圃 2019
統計学の基礎としての確率論という内容で、確率測度の性質を解説しています。
起こりうる頻度の比を確率として定義するのは、ラプラス流で、頻度論的確率。
ラプラス流の確率が持つ自然な性質を失うことなく、より一般の事象に対する確率として定義したのが、コルモゴロフ。
σ加法族の写像として確率を定義する。これは、公理論的確率論と呼ばれる。
以下は、タイトルにも測度論との結び付きが見えるような本です。 統計学の教科書的な本はたくさんあるので、確認できていませんが、いくつか見た感じだと、 確率測度の定義から説明を始めている統計学の本は、他にもたくさんある印象です。
「統計科学の基礎 データと確率の結びつきがよくわかる数理」 白石高章 著 日本評論社 2012
測度の説明はありませんが、確率測度の定義から始まり、その性質を説明した後で、確率変数などの説明になります。
「測度論からの数理統計学」 綿森葉子・田中秀和・田中潮 著 共立出版 2023
統計学の教科書のようにして書かれています。
タイトルに「測度論」と入っていますが、測度の話は少しでした。
順路
次は
人工知能（AI）
