図で「元データ」と書いている点は、個々のサンプルの値です。 そのため、「次にサンプリングしたら、どのくらいの値になるだろうか？」、という疑問が起きます。 この値は、未来の予測をしたい場合に重要になります。
統計学を使った予測は、統計学の分野ではそれほど扱われませんが、 機械学習 の分野では、中心的な方法になっています。
機械学習では、点推定の予測値がよく使われますが、予測は区間として出す方法があります。
ちなみに、統計学における「予測（predict）」は、必ずしも未来のデータの推定のことではないです。
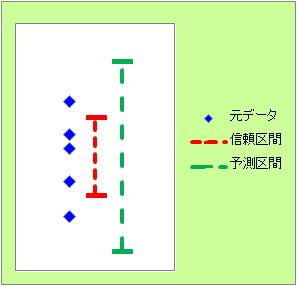
図で「元データ」と書いている点は、個々のサンプルの値です。
そのため、「次にサンプリングしたら、どのくらいの値になるだろうか？」、という疑問が起きます。
この値は、未来の予測をしたい場合に重要になります。
その疑問に答えるのが予測区間です。 予測区間とは、「ある確率で、個々のサンプルの値があると考えられる区間」です。 図では、95%の確率の場合を描いてみました。
になります。
予測区間は、「1+1/n」という部分がありますが、 信頼区間 と似た作りになっています。 信頼区間は、nが非常に大きいとゼロに近付きますが、「1+」の部分があることで、nが非常に大きい時にルートの中は１に近付きます。
nが大きい時の予測区間は、データを確率分布で近似することと、変わらなくなって来ます。
新しいサンプルの値が、この区間に入っていれば、想定内の結果ということになります。 区間の外だとすると、もしかしたら、異常状態のデータかもしれません。
予測区間には、 外れ値の判定 や 異常値の判定 の方法としての使い道があります。
判定をする時には、目安になる数値（閾値）が必要です。 その数値の根拠として、予測区間が使えます。
予測区間は、正規分布のような１次元分布以外でも、役に立ちます。
回帰分析系では、回帰式の予測値がどのくらいの精度なのかを知るのに、予測区間が目安になります。
回帰分析の予測区間
と
比例分散の予測区間
のページがあります。
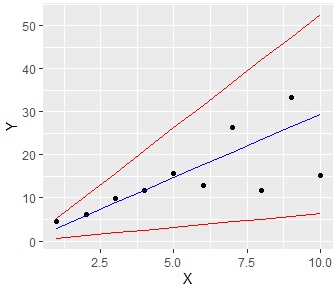
予測区間の幅の決まり方には、特徴があります。
予測区間を実務で使おうとすると、「こんなに幅が広いと、当てにならないから、ちょっと使えないなぁ。。。」、 ということがあります。 区間を狭めるには、これらの性質を考えます。
単純に区間の見た目を狭めたいのであれば、確率をいじれば良いです。 実用的な目的を考えるのでしたら、サンプルを増やしたり（「ｎ数を増やす」とも言います）、 標準偏差の大きさの原因（データのばらつき）の原因を調べて、標準偏差を小さくする必要があります。
予測区間は、サンプル数が影響するのは、スモールデータの時だけで、ある程度大きくなると、影響がほとんどなくなります。
下のグラフは、平均値が０で、標準偏差が１の場合の、95%予測区間です。サンプル数の影響がわかるようにしてあります。
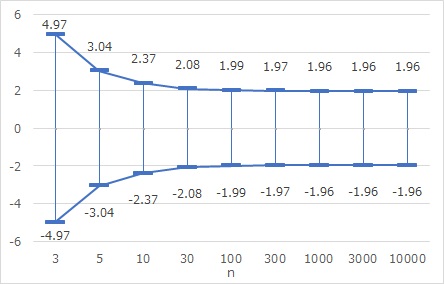
予測区間の計算式には、t分布が入っていたり、nの影響があったりしますが、n=30を超えて来ると、 正規分布の95%の区間とほとんど変わらなくなります。
このため、予測区間が役に立つのは、サンプル数が一桁くらいのスモールデータの時だけです。 スモールデータの時は、サンプル数が少ないことによるあいまいさが、予測区間の広さとして現れるようにした使い方ができます。
Rの実施例は、 Rによる予測区間の分析 にあります。
このページは、正規分布の信頼区間と予測区間で、計算シンプルです。 Rによる予測区間の分析 には、 回帰分析の予測区間 の例もあります。
R-EDA1 でもできます。
「Similarity_of_Variables_and_Categories（変数やカテゴリの類似性）」
→「Between_label_column_and_others（ラベルのと他の変数の関係）」
→「Stratifeid_graph（）
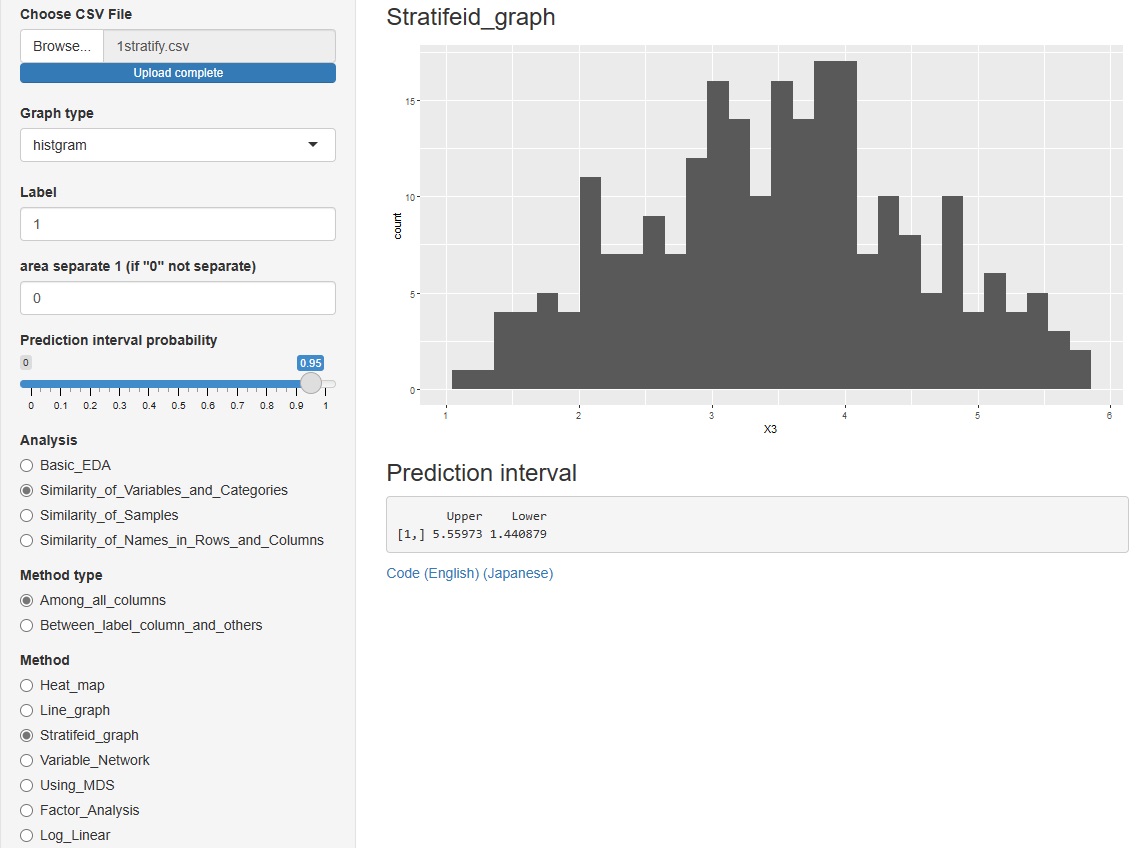
と進んだ中にある「histgram（ヒストグラム）」で予測区間を出すようにしました。
ただし、グラフを層別した時には、計算されません。
ヒストグラムは、区間が数字で表示されます。
順路
次は
ロバスト推定
