推定 の理論は、統計学を普段使う人でも、使わない人はまったく使わないようなものかもしれません。 筆者の場合、信頼区間の理論が役に立った経験はないのですが、予測区間は役に立った経験が何度かあります。
Rを使う場合は、 予測のためのソフトの使い方 の応用になります。
この例は、95%の予測区間を求める方法です。
予測区間
のページにある予測区間の例を、Rで実行する場合になります。
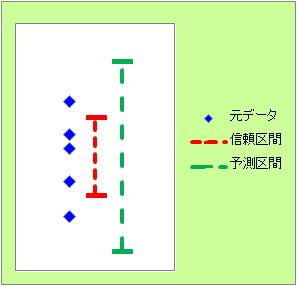
Rの使用例は下記になります。 下記は、コピーペーストで、そのまま使えます。 この例では、Cドライブの「Rtest」というフォルダに、 「Data.csv」というファイルがあり、１列目だけにデータが入っている状態を想定しています。 １行目から数値データが入っていて、変数名は入っていない状態を想定しています。
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=F) # データを読み込み。１行目も数値データとして読み込み
M <- mean(Data[,1])# 平均値
n <- nrow(Data)# サンプル数
t <- -qt((1-0.95)/2, n-1)# t値
V <- var(Data[,1])# 分散
Upper <- M + t * sqrt(V * (1 + 1/n)) # 予測区間の上側
Lower <- M - t * sqrt(V * (1 + 1/n)) # 予測区間の下側
Upper# 予測区間の上側を表示
回帰分析の予測区間 も推定できます。
Rの使用例は下記になります。 下記は、コピーペーストで、そのまま使えます。 この例では、Cドライブの「Rtest」というフォルダに、 「Data.csv」という名前でデータが入っている事を想定しています。
また、目的変数として「Y」、説明変数として「X」という名前の変数が、データに入っている事を想定しています。
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # 学習データを読み込み
lm <- lm(Y ~ ., data=Data) # 学習データで回帰分析
X <- 6 # 予測区間を求めたいXの値を入力
X <- as.data.frame(X)# データフレームに変換
predict(lm, X , interval="prediction", level = 0.95) # 予測区間を計算
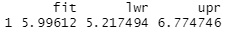
回帰式で求めた予測値（fit）と、予測区間の上側（upr）、下側（lwr）が出力されます。
例えば、「上側が6.77なので、X = 6の時に、Y = 6だったら正常値。Y = 7だったら異常値 」という風に、 異常値の判定 に使えます。
library(ggplot2)# ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # 学習データを読み込み
lm <- lm(Y ~ ., data=Data) # 学習データで回帰分析
Data1 <- predict(lm, Data, interval="prediction", level = 0.95) # 予測区間を計算
Data2 <- cbind(Data, Data1) # 元データと予測区間の計算結果を結合する
ggplot(data = Data2, aes(x = X, y = Y)) +geom_point()+geom_line(aes(y=lwr), color = "red")+geom_line(aes(y=upr), color = "red")+geom_line(aes(y= fit), color = "blue") # グラフを出力
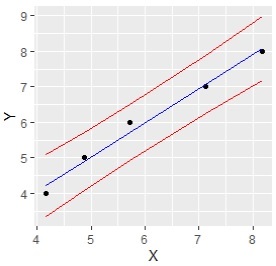
このグラフでも例えば、「X = 6の時に、Y = 6だったら正常値。Y = 7だったら異常値 」という風に、 異常値の判定 に使える点は同じです。
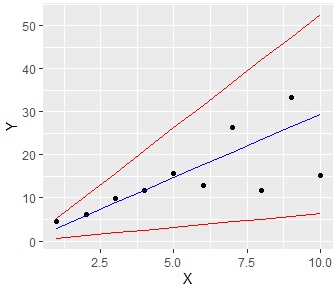
比例分散の予測区間 の場合です。
library(ggplot2)# ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # 学習データを読み込み
M <- mean(Data$Y / Data$X)# 平均値
n <- nrow(Data)# サンプル数
t <- -qt((1-0.95)/2, n-1)# t値
V <- var(Data$Y / Data$X)# 分散
Upper <- M + t * sqrt(V * (1 + 1/n)) # 予測区間の上側
Lower <- M - t * sqrt(V * (1 + 1/n)) # 予測区間の下側
upr<-Data$X * Upper
lwr<-Data$X * Lower
fit<-Data$X * M
Data2<-cbind(Data,lwr,upr,fit)
ggplot(data = Data2, aes(x = X, y = Y)) +geom_point()+geom_line(aes(y=lwr), color = "red")+geom_line(aes(y=upr), color = "red")+geom_line(aes(y= fit), color = "blue") # グラフを出力
