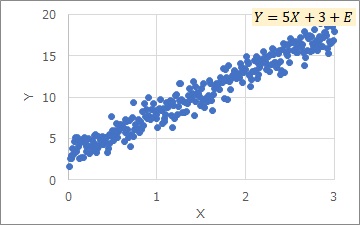
As illustrated on Single Regression Analysis page, regression analysis is based on a model based on the assumption of four points: "residuals are homovarious", "residuals are normally distributed", "approximate by a straight line", and "linear sum (additive)". This is exactly the case with the data shown in the figure below.

There are ways out there that don't fit these assumptions. For example:
The generalized linear model is a theory that generalizes the three assumptions of "residuals are homodispersed", "residuals are normally distributed", and "approximated by a straight line". However, since it is not a theory that "non-uniform variance, non-normal distribution, non-linear is anything OK", it does not mean that regression analysis of proportional variance, regression analysis of curves, and multiplicative models will be unnecessary.
Y = AX+B
Raise
Y=g(AX+B)
By making g() an arbitrary function, it can be used for curves.
The inverse of g() is f().
f(Y) = AX+B
is called a link function.
The link function defaults to common combinations in the world, such as "identity function when it is normally distributed" and "logarithm when it is Poisson's distribution".
The generalized linear model assumes any distribution other than the normal distribution as the distribution of the residuals.
In the software, you can choose from it.
If the Poisson distribution is assumed, it is called Poisson regression model. If you assume a binomial distribution, it is the same as Logistic Regression Analysis.
Responses other than non-constant variance are linked to responses other than normal distributions.
For example, the Poisson distribution is the square root of the mean magnitude of the variance. Since the regression equation is an expression that shows the value of the mean value at each X, the magnitude of the variance also changes for each X. If the model has a larger mean as X increases, then the larger X the larger the variance. This makes it not evenly distributed.
Generalized Linear Mixed Model is an extension of the Generalized Linear Model.
Generalized linear model software can be found on Generalized Linear Mixed Model page.
