自己相関分析

「相関」と言えば、ふつうは「XとYの相関」という感じで、異なる変数の関係を調べますが、自己相関分析では、基本的にひとつの変数の中だけの話です。「自己」との相関を調べますので、自己相関分析と言います。

自己相関分析では、Xになるのが、前の測定の値とか、１時間前の値になります。前の測定データには、さらに前のデータがありますから、同じ値が、別の値のXになったりYになったりします。

自己相関の調べ方

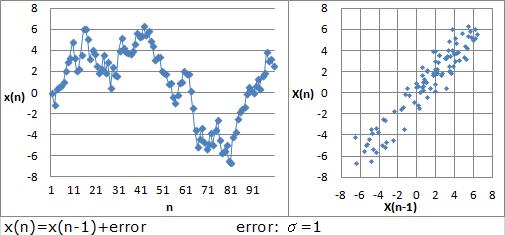
図の折れ線グラフのデータの場合、あるステップの値をX(n)、１つ前のステップの値をX(n-1）として、 X(n)とX(n-1）の２次元散布図を描くと、図の散布図になります。この散布図では、XとYの相関性を見る時と同じようにして、X(n)とX(n-1)の関係を見ています。

自己相関が高いと、相関が高い時と同じように、データが直線状に並んでいます。

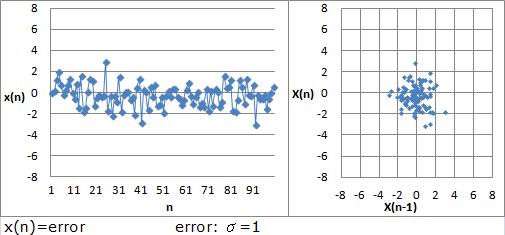
自己相関が低いと、散布図からも相関が見られないです。

XとYのように、異なる変数の相関性（単相関）の話ではなかったことが、自己相関にはあります。

それは、自己相関が高くなるのは、X(n)とX(n-1)の値が近い場合ということです。

この事を使うと、応用範囲が広がります。

「自己相関が高くなるのは、X(n)とX(n-1)の値が近い」、という事は、
「自己相関が高い　＝　値がほぼ連続的につながっている」
という意味にもなります。そこで、自己相関が、連続性の尺度に使えます。

連続性の尺度は、解析しようとしているデータに、時系列の特徴があるのかどうかの確認に使う事もできます。

データに周期性があると、1ステップ前以外の値との自己相関も高いことがあります。

この性質を使うと、n-1、n-2、n-3、、、という風に、順番に検証していくことで、周期を見つけることができます。例の場合だと、18のステップで、1つの周期になっていると言えます。
自己相関

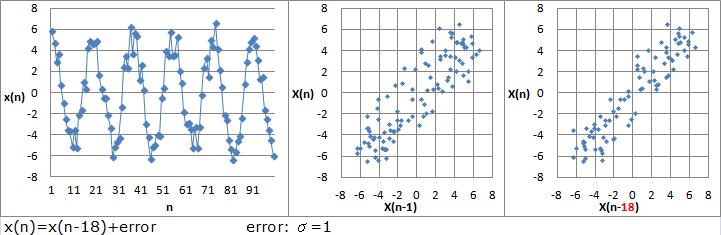
「自己相関が高い　＝　最新のデータが、未来のデータに一番近い」ということになります。そこで、自己相関が高いことを根拠として予測ができるようになります。

１ステップ前のデータとの自己相関が高いのなら、１ステップ前のデータが予測値です。１周期前のデータとの自己相関が高いのなら、１周期前のデータが予測値です。

自己相関を根拠にする予測は、時系列近傍法の基本です。

ここまでは、ある時点（ステップ）の値と、１つ前のステップの関係を調べる方法として、自己相関分析を説明しています。

理論は、単回帰分析を応用してています。

重回帰分析を応用した場合もあり、 SARIMAX として開発されて来ています。ただし、SARIMAXのMAの部分は、一般的な重回帰分析では解けないです。