 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
「独立ならば相関がない」と考えると、2つのランダムウォークモデルから作られるデータは、相関がないはずです。
しかし、実際は、相関係数が-1から1まで幅広くなってしまうことが知られています。 この現象は、「見せかけの回帰」と呼ばれています。
世の中で、「見せかけの回帰」と呼ばれているものは、いくつかあります。 これらが混同されて説明されることもあります。
このページで、以下で説明するのは、「非定常な時系列データで、高確率で起こる現象」についてです。
非定常な時系列データで、高確率で起こる場合の、見せかけの回帰は、例えば、下のようなものです。
左の折れ線グラフが、時系列の変化を表しています。右の散布図は、左のグラフのデータを使っています。
XとYが何となく似たカーブになっていますが、それによって、相関係数が大きくなっています。
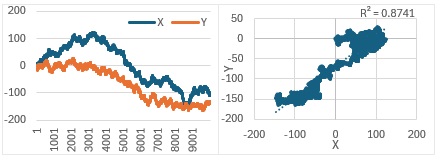
まず、下記のランダムウォークモデルで生まれたデータなので、XとYが何となく似たカーブになるモデルではないです。
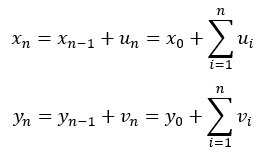
上のグラフを見ると、「サンプル数が少ないため、データの相関が高くなった」、「XとYの両方が時系列に対して相関するモデルになっているため、XとYが疑似相関の関係になった」、「外れ値によって、相関係数が大きくなった」、「相関があるように見えるデータだけを選んだ」、「回帰係数の検定で相関の有無を判断している。そのため、相関係数が小さくても、P値が小さければ「相関あり」と判断している」という場合でないことは、一目瞭然です。
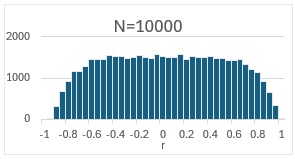
下のヒストグラムは、上のように10000ステップあるランダムウォークをランダムに発生させる試行を5000回して、相関係数rを求めたものです。
このグラフから、「サンプル数は十分多いが、ごくまれに起きる相関が高い状況が、たまたま起きてしまった」ではないことと、
「非定常な時系列データで、高確率で起こる現象」であることがわかります。
なお、「高確率で相関係数が大きくなる」と表現しましたが、「相関係数が0にはならなくなる(なりにくくなる)」という意味ではないです。
統計学の一般的な解説では、暗黙の前提として「データは定常」という条件があります。 定常というのは、平均値や分散(標準偏差)が、時間が経っても変わらないことです。
定常なデータの場合、サンプル数が増えれば増えるほど、平均値や分散がどこかの値に収束して行きます。
一方で、ランダムウォークは非定常です。 サンプル数が増えても、平均値や分散が収束しません。
非定常なデータでは、「独立ならば、相関がない」という法則が成り立たないです。 「見せかけの回帰」と呼ばれる現象が起きます。 これは、「独立ならば、相関がない」という法則を導き出す時に、非定常性が考慮されていないために起きている矛盾です。
見せかけの回帰は、時系列データでは頻繁に起きる現象なので、「起きるか・起きないか」ということは、簡単にシミュレーションできます。
ところが、この現象が起こる理由について、既存の文献を調べたのですが、筆者が納得できる説明は見つけれられていません。
「ランダムウォークでは、回帰係数の検定をすると、有意になりやすい」ということについて、数学的な説明をしている資料はあります。 しかし、サンプル数が増えれば回帰係数の検定が有意になりやすいのは、ランダムウォークに限定される話ではないので、筆者の探しているものとは違いました。
そこで、筆者は自分で考えてみました。今のところ、以下の説明で良いのではないかと考えています。
以下では、 逐次学習 からのアプローチで、見せかけの回帰で起きていることを数式で説明します。
平均値の逐次学習の式を、下のように変形します。
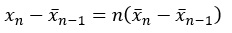
変形した式を、共分散の逐次学習に代入します。
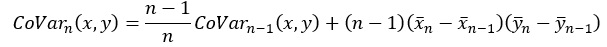
変形した式を、相関係数を求める式に代入します。
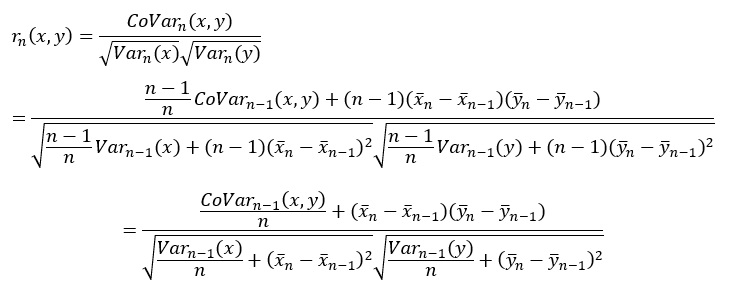
xとyが定常過程の場合は、定義から
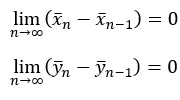
となるので、
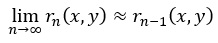
となります。これは、相関係数がひとつの値に収束することを表します。
非定常過程の場合は、定常の時に消える項が残るので、相関係数が収束しないことを表している式になります。つまり、相関係数が変化し続けることを表します。
相関係数が変化し続けるので、相関係数が0の近くになっても一時的です。また、ある瞬間については、相関係数の絶対値が大きいこともあります。これが見せかけの回帰です。
順路


 次は
ARMAモデル
次は
ARMAモデル

