反実仮想データの取得 のページでは、上のようなデータを例にして、反事実のデータを取得する話があります。
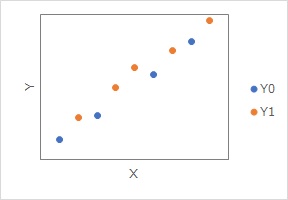
反実仮想データの取得
のページでは、上のようなデータを例にして、反事実のデータを取得する話があります。
下のようなデータの場合は、Y0のデータが取れているXの範囲と、Y1のデータが取れているXの範囲がずれています。
このような場合は、何らかの方法で反事実のデータを推定したとしても、
Yの値の違いが、Y0とY1の違いによるものなのか、Xの範囲の違いによるものなのかが区別できません。
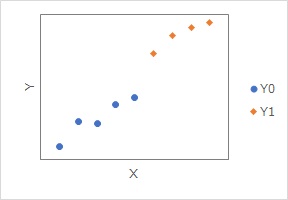
Ｘに相当するものが１変数の場合は、上のグラフのようにすれば、妥当な反事実のデータが取れるかが確認できます。 Ｘが２次元以上、つまり、複数の変数がある場合は、この方法が使えません。
そこで、確認方法を考えてみました。 （どこかの文献に同じような方法があれば、ご教示いただけると幸いです。）
３つ考えてみましたが、２つは サンプルの類似度の分析 を使います。
高次元を２次元に圧縮して可視化 の応用です。
まず、高次元のデータを２次元データにします。
そして、２次元散布図の中で、Y0とY1のデータの混ざり方を確認します。 完全に分かれているようなら、先には進めません。
下は、R-EDA1
を使った分析例です。
この場合は、0と1がだいたいまんべんなく混ざっているので、反事実のデータの推定に進んでも、良さそうです。
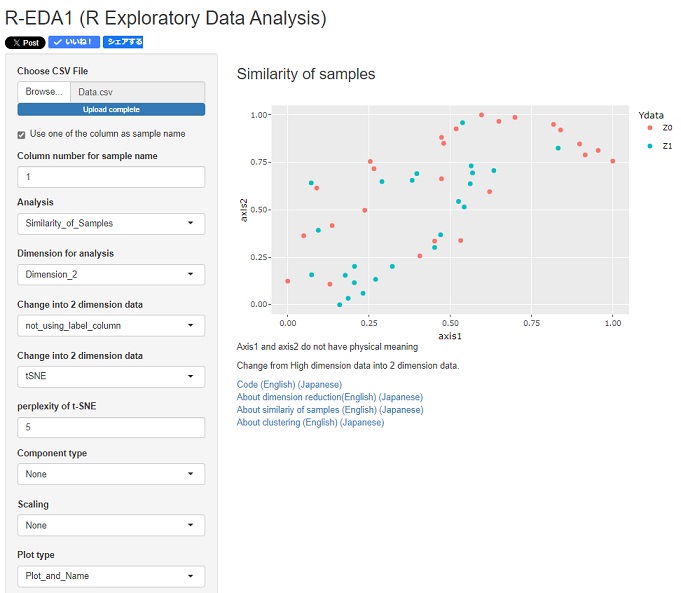
R-EDA1で、この分析をするには、Yの変数を削除して、ZとXの変数だけにする処理と、 Zの「0」は「Z0」などの、質的変数に処理しておきます。
クラスター分析 の応用です。
まず、高次元のデータを、クラスター（１次元の質的データ）にします。
そして、クラスター毎にY0とY1の割合を確認します。 0と1のデータなら、平均値がY1の割合を計算していることになります。
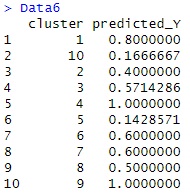
下は、 Rによるベクトル量子化平均法 のページのコードを使って、10個のクラスターに分けて、それぞれの平均値を計算した結果です。
平均値が1.0の領域もありますが、反事実のデータの推定に進んでも、良さそうです。
ロジスティック回帰分析 などの、 ラベル分類 の応用です。
統計的因果推論 では、 傾向スコア の計算に、 ロジスティック回帰分析 を使う方法があります。 この方法を使う時は、モデルに合うかどうかが大事な確認になります。 合わないのなら使えないです。
反実仮想データ取得の確認を目的として使う時は、モデルに合わないかどうかが大事な確認になります。 合わないのなら、「反事実のデータの推定に進んでも、良さそう」となります。 合う場合は、「確率がほぼ1.0の領域と、ほぼ0.0の領域は、反事実のデータの推定ができない領域」といったようにして考える必要があります。
順路
次は
反実仮想機械学習
