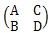
という行列があって、
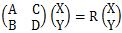
が成り立つ時、Rを固有値、(X,Y)を固有ベクトルと言います。
このページの 一対評価 は、比(A / B)や差(A - B)を評価する方法です。
AやBを単独で計測することは難しくても、相対評価ならできる時に便利です。
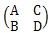
という行列があって、
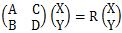
が成り立つ時、Rを固有値、(X,Y)を固有ベクトルと言います。
固有値と固有ベクトルの計算は、あまり表に出て来ることがありませんが、 例えば、 主成分分析 で、主成分を見つけるのに使われます。
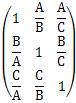
という行列があるとします。
対角成分が逆数になっていて、特殊な行列です。
唐突ですが、
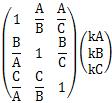
、という計算をするとします。
すると、
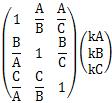
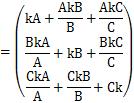
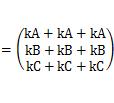
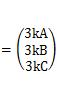
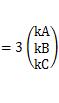
、となります。
この式の最初と最後を見ると、
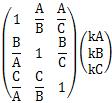
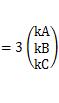
、となりますので、この行列の固有値は3、固有ベクトルは、(kA,kB,kC)であることがわかります。
固有値の3は、3行3列の行列である事から決まりますので、n行n列の行列なら、固有値はnになる事が一般的に言えそうです。
一般的に、固有値と固有ベクトルを求める計算は、それなりに手間がかかるのですが、 上記のような行列の場合は、計算をしなくても固有値がわかります。 また、固有ベクトルは、行列の成分を計算する数字と同じものが使われている点もポイントです。
(A,B,C)=(5,2,1)
のように、横並びの値がわかっているのなら不要なのですが、
世の中には横並びの値を測る事が難しい場合があります。
しかし、もしも、A/B、A/C、B/Cの値を知る事ができるのなら、上記の特殊な行列に当てはめる事で、
(kA,kB,kC)
の値はわかります。
残念ながら、kはわからないので、(A,B,C)の値そのものはわからないのですが、 A、B、Cの順番や離れ具合は、わかります。
もちろん、何らかの方法でkがわかれば、(kA,kB,kC)の値を使って、(A,B,C)を計算する事もできます。
このようにして、一対評価をすることで、横並びの値を計算することができます。 横並びの値ができれば、 多変量解析や データマイニング による解析もできるようになって来ます。
A/C、B/Cの値があれば、固有値の計算を使わなくても、(kA,kB,kC)は求まります。
(A/C,B/C,C/C) = (A/C,B/C,1) = (kA,kB,kC)
しかし、これにさらに、A/Bがあった場合に、上記の計算から求めた A/Bと、計算が合わない可能性があります。
固有値の計算を使えば、3つの測定値から、(kA,kB,kC)のそれらしい値を求めることができます。
AHP は、横並びの値を取ることが難しい項目について、一対評価で横並びの値を求めることを、積極的にしていく手法の代表的なものです。
AHPで行列に逆数が登場するのは、特殊な行列を使うことを意識しているからのようです。
AHPでは、一対評価として、A/B、A/C、B/Cという「比」を推定する事はしないで、 「AとBの差」を評価します。 これは、一対評価をやりやすくする工夫と考えられます。
順路


 次は
フェルミ推定
次は
フェルミ推定

