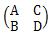
When there is a matrix that
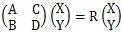
The paired evaluation on this page is a method of evaluating ratios (A / B) and differences (A-B).
Even if it is difficult to measure A and B independently, it is convenient when relative evaluation is possible.
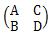
When there is a matrix that
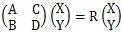
holds, R is called an eigenvalue and (X, Y) is called an eigenvector.
Eigenvalue and eigenvector calculations are rarely exposed, but are used, for example, in principal component analysis to find principal components.
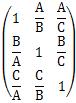
Suppose there is a matrix called. It is a special matrix with the reciprocal of the diagonal component.
It's abrupt, but
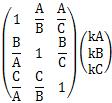
let's say you want to calculate. Then,
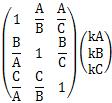
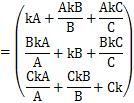
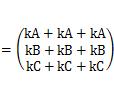
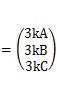
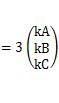
becomes.
Looking at the beginning and end of this equation, we
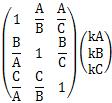
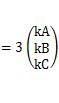
know that the eigenvalues ??of this matrix are 3 and the eigenvectors are (kA, kB, kC).
Since the eigenvalue 3 is determined by the fact that it is a matrix with 3 rows and 3 columns, it seems that it can be generally said that the eigenvalue is n for a matrix with n rows and n columns.
In general, the calculation to find the eigenvalues ??and eigenvectors takes some time, but in the case of the above matrix, the eigenvalues ??can be found without any calculation. Another point is that the eigenvectors are the same as the numbers used to calculate the components of the matrix.
It is unnecessary if you know the side-by-side values ??like (A, B, C) = (5,2,1) , but it may be difficult to measure the side-by-side values ??in the world.
However, if you can know the values ??of A / B, A / C, B / C, you can find the value of (kA, kB, kC) by applying it to the above special matrix .
Unfortunately, I don't know k, so I don't know the value of (A, B, C) itself, but I know the order and distance of A, B, C.
Of course, if you know k in some way, you can also use the value of (kA, kB, kC) to calculate (A, B, C).
In this way, you can calculate side-by-side values ??by performing pair evaluation. If side-by-side values ??are created , multivariate analysis and data mining analysis will be possible.
If there are A / C and B / C values, (kA, kB, kC) can be obtained without using the calculation of eigenvalues.
(A / C, B / C, C / C) = (A / C, B / C, 1) = (kA, kB, kC)
However, if there is an A / B in addition to this, there is a possibility that the calculation does not match the A / B obtained from the above calculation.
Using the eigenvalue calculation, you can find the likely value of (kA, kB, kC) from the three measurements.
AHP is a typical method of proactively finding side-by-side values ??by paired evaluation for items for which it is difficult to take side-by-side values.
It seems that the reciprocal appears in the matrix in AHP because it is conscious of using a special matrix.
AHP does not estimate the "ratio" of A / B, A / C, and B / C as a pair evaluation, but evaluates the "difference between A and B". This is considered to be a device that makes pair evaluation easier.
NEXT 

 Ferimi Estimation
Ferimi Estimation
