ハイブリッド有向相関分析 と似た方法には、 LiNGAM や ベイジアンネットワーク があります。
先に結論から書けば、実務で、データの構造を調べる時にメインで使うと良いのは、ハイブリッド有向相関分析です。
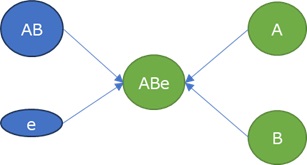
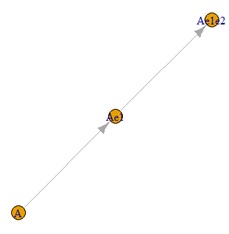
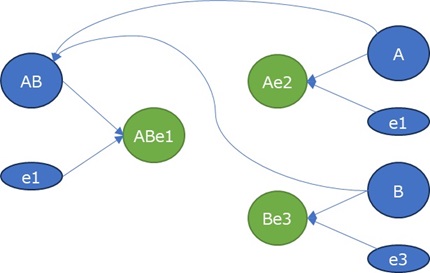
左から順に、データの構造、ハイブリッド有向相関分析、LiNGAM、ベイジアンネットワークです。
分析の対象は、緑色の変数です。 青色の変数は、緑色の変数の要素です。
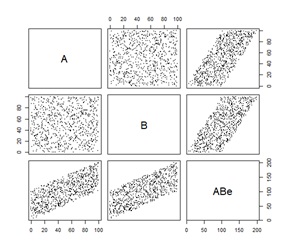
重回帰分析のモデルが想定しているデータになっています。
３つとも、正しく構造を導いています。
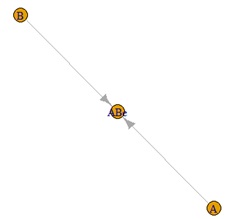
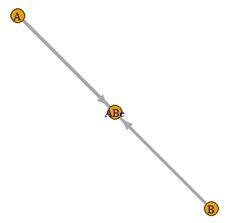
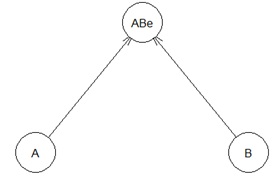
Ae1とAe2が擬似相関の関係になっています。
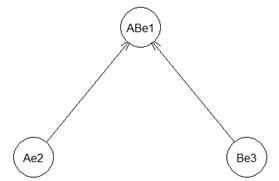
欲しい結果を出せたのは、ハイブリッド有向相関分析だけです。 LiNGAMは、間違った方向を出しています。 ベイジアンネットワークは、元々この構造の場合、矢印の方向を決められないです。 矢印はないですが、Ae1とAe2の間に線がないので、間違いはしていません。
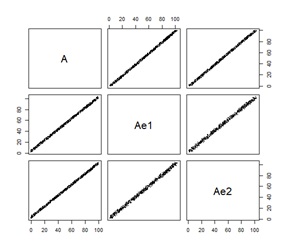
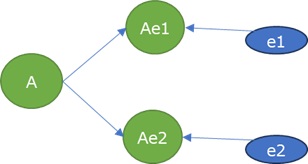
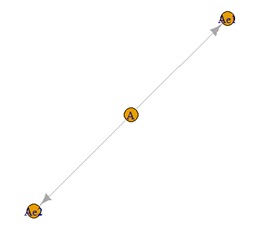
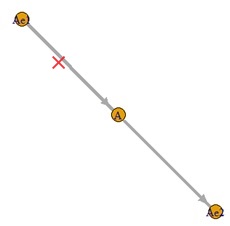
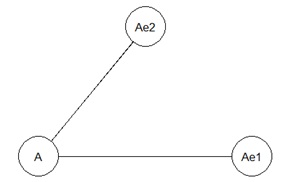
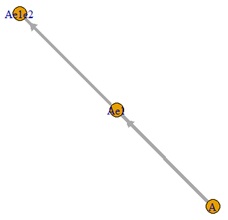
欲しい結果を出せたのは、ハイブリッド有向相関分析とLiNGAMです。 ベイジアンネットワークは、元々この構造の場合、矢印の方向を決められないです。 矢印はないですが、AとAe1e2の間に線がないので、間違いはしていません。
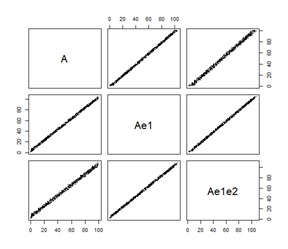
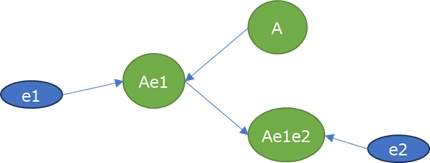
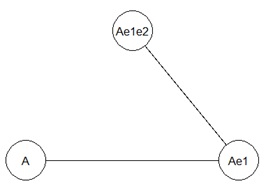
ハイブリッド有向相関分析とベイジアンネットワークは、矢印は出ませんが、間違っていない結果を出しています。 LiNGAMは、矢印の向きが間違っています。
なお、この例でのハイブリッド有向相関分析の結果は、正確にはハイブリッド有向相関分析の結果ではなく、 その前段で行っている 相関偏相関分析 の結果です。
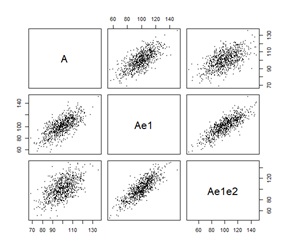
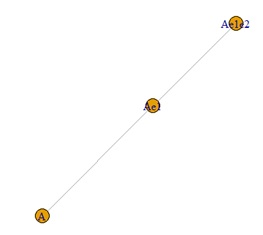
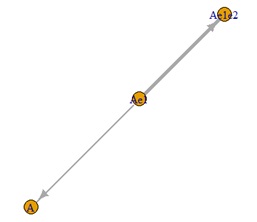
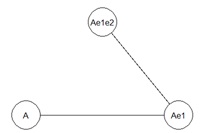
どの方法でも、欲しい結果が出ました。 実務のデータでは、３変数のどれにも誤差が加わっている場合が普通なので、良い結果です。
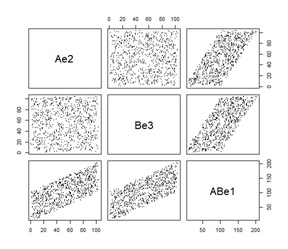
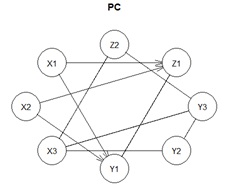
上のグラフから、左から順に、元データの散布図、元データの構造、ハイブリッド有向相関分析、LiNGAM、ベイジアンネットワークです。
ベイジアンネットワークは、ここだけ２つあります。
左が量的変数をそのまま分析したもので、右が質的変数に変換してから分析したものです。
欲しい結果を出せたのは、ハイブリッド有向相関分析だけです。 向きの間違いはなく、過不足もないです。
LiNGAMとベイジアンネットワークは、不正確な結果になりました。 ベイジアンネットワークによる構造探索のアルゴリズムの違い のページで詳しく調べていますが、ベイジアンネットワークでは、量的変数は、質的変数に変換すると、結果が良くなることが多いです。 しかし、上の例の場合は、改善らしい改善は見られませんでした。
ハイブリッド有向相関分析は、 Rによる有向相関偏相関分析 に、上記の実施例のコードがあります。
LiNGAMは、RによるLiNGAMのコードを使っています。 前処理に標準化は使っていません。
ベイジアンネットワークは、 Rによるベイジアンネットワーク のコードを使っています。アルゴリズムは、pc.stableです。 前処理に質的変数への変換はしていません。
順路
次は
LiNGAM
