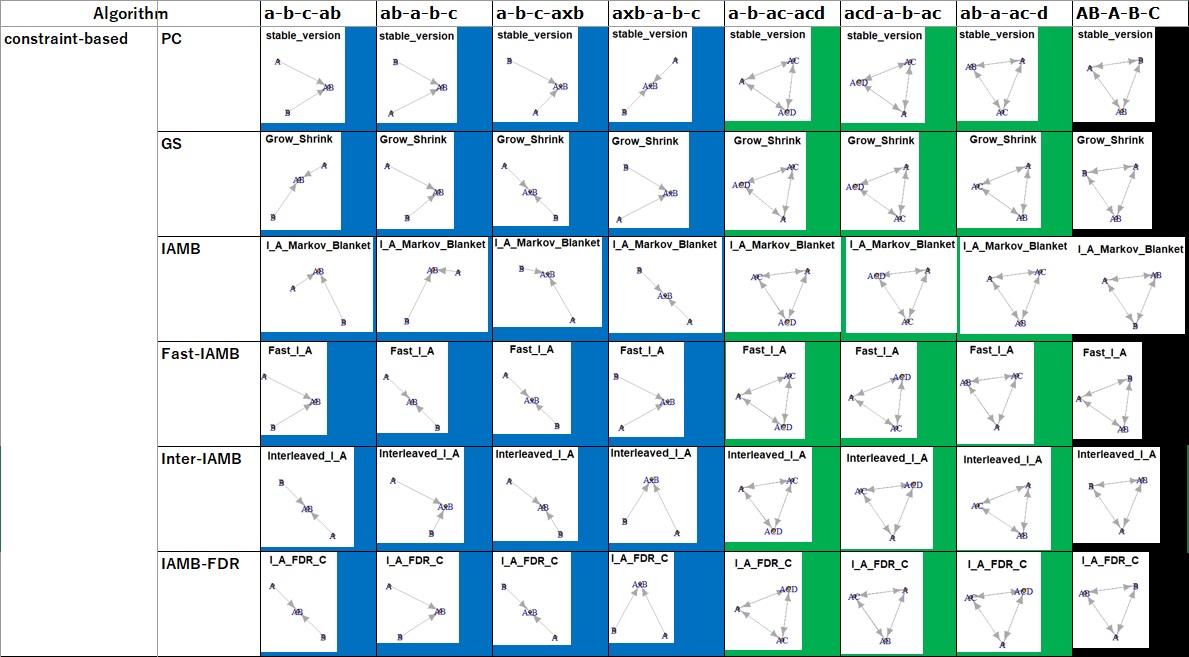
ベイジアンネットワークによるデータの構造解析 のアルゴリズムは、いろいろあります。
「データの構造を調べる」という分析を目的にしている時に、どのアルゴリズムが良いのかを調べたのがこのページになります。
まず、結論は「アルゴリズムは、PCが一番良い。」になります。
また、この調査の中で、どのアルゴリズムを使うとしても、量的変数は、質的変数に変換してから分析した方が良いことも確認しています。
サンプル数は、サンプルが足りなかったから、正しい結果が出せないとならないように、10000にしています。
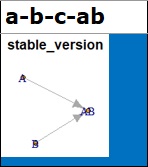
例えば、表の中で、「a-b-c-ab」という列は、変数が左から順にA、B、C、ABとなっている表について、質的変数にしています。
「a-b-c-ab」、「ab-a-b-c」は、変数の並び方だけが違います。 この調査では、変数の並び方の違いも調べています。
セルが青の場合は、本当の構造とグラフが同じ場合です。
この例では、AとBでABを作っているので、AかAB、BからABに矢印があって、Cはどことも結び付かないのが正解なのですが、その通りになっています。
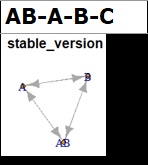
セルが黒の場合は、絶対に出して欲しくない結果になった場合です。
この例では、AとBは独立しているので、結び付かないのが正解なのですが、結び付いています。
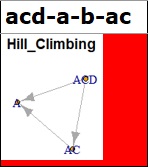
セルが赤の場合は、間違いな点は黒と同じです。
この例では、例えばACからAを作っていないのに、ACからAに矢印が付いています。
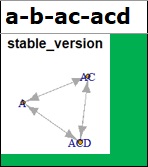
セルが緑の場合は、データの背景を突き止めるところまではできないものの、ある程度考察できるようになる結果になった場合です。
データだけでは矢印の向きが決められないのなら、結び付けることだけをして向きは決めてくれない方が、後の分析で間違わないので助かります。
上の赤の例のデータの場合、この緑のようなグラフになるのが、分析としては理想です。
アルゴリズムは、Rのbnlearn、BNSL、dealのパッケージを使っています。 下記で、「BNSL」、「deal」となっているもの以外は、すべて、bnlearnのアルゴリズムです。 Rによるベイジアンネットワーク のコードを使っています。
パラメタはデフォルトを使っています。
量的変数を使っているAB-A-B-C以外では、青または緑になっています。
このグループがベストなので、このページの冒頭の結論になっています。
条件付き独立性検定には、有意水準のαがあり、何も指定しないと0.05がデフォルトとして使われます。 量的変数のままだと、辺がたくさん出て来るのは、量的変数の方が、0.05よりも低くなりやすいためです。
constraint-based系(1)で青にできることが、緑になっています。
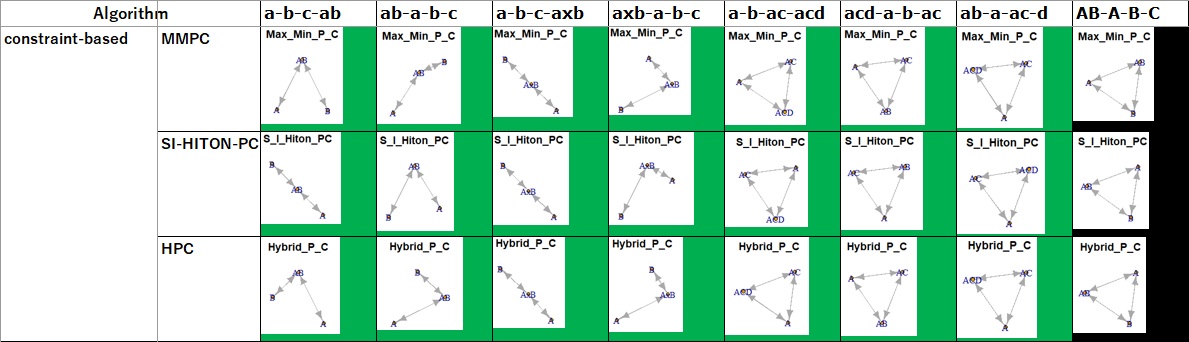
変数の順番が違うだけで、青になったり、赤になったりします。
この特徴の使い道があるかもしれませんが、データの順番の意味があるのかどうかもわからないデータの分析には、不向きなアルゴリズムです。
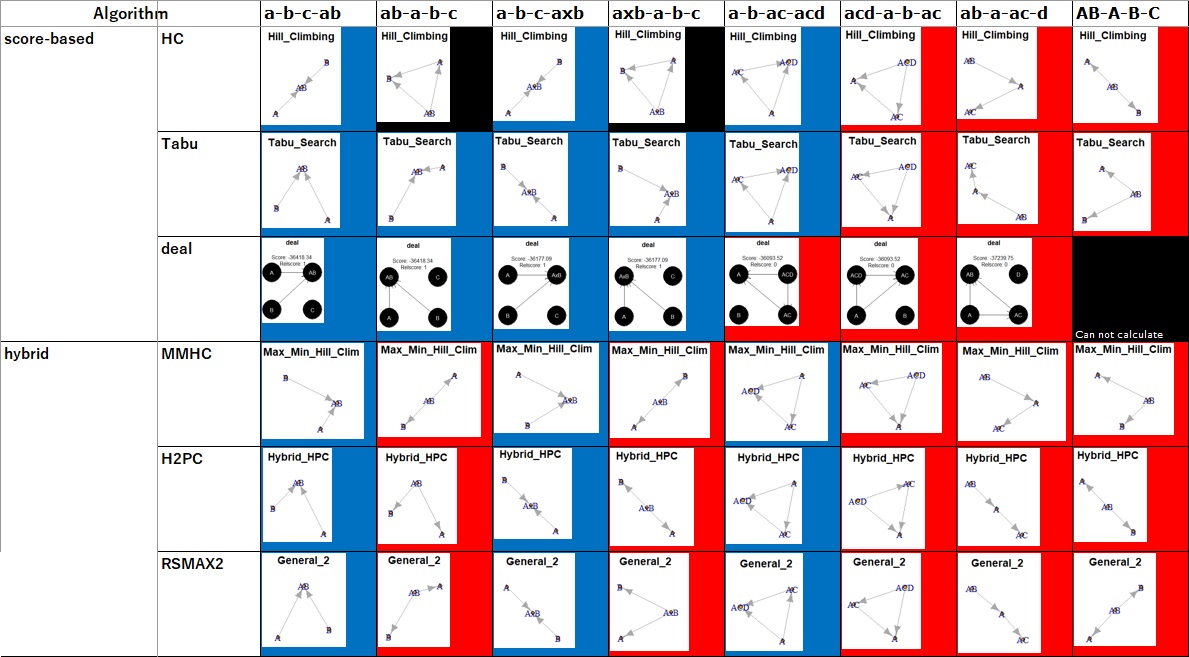
黒が多いので、この使い道だと、使えないです。
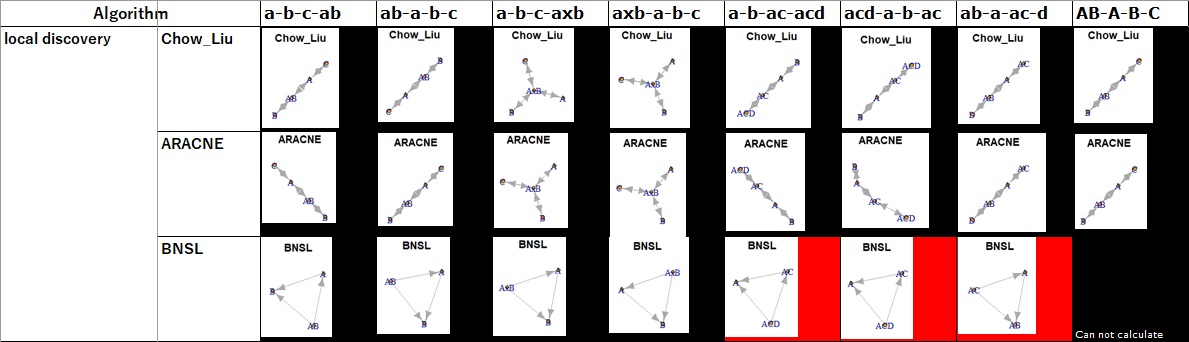
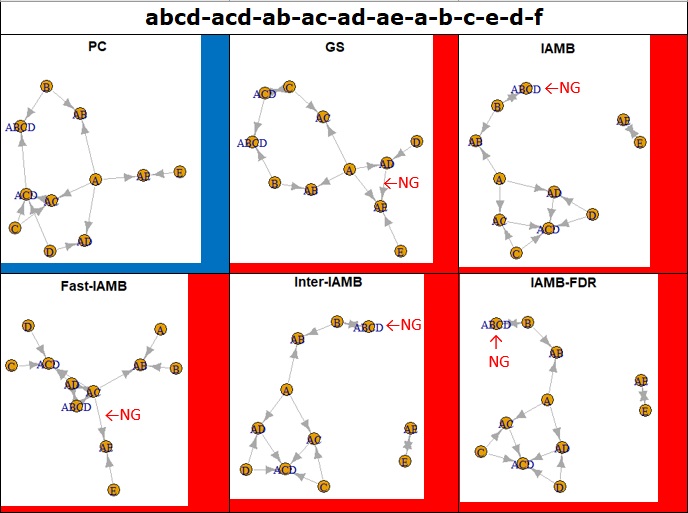
アルゴリズムの比較(1)で、条件付き独立性検定（constraint-based）系のグループが良いことがわかりましたが、 このグループの中での違いはわからないです。
もう少し複雑なデータで試してみたところ、一番良いのは、PCということがわかりました。
他のものは、結び付いて欲しくないところが結び付いたり、矢が集まって来て欲しいABCDが孤立したりしました。
順路
次は
ベイジアンネットワークによる構造探索のノウハウ
