符号反転の条件式

符号反転は、「多重共線性」や「シンプソンのパラドックス」といった理由ではなく、符号反転の条件式が成り立っている時に起きます。

符号反転の条件式は、以下の式です。

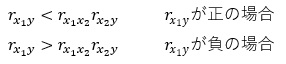
この式の「r」は、相関係数です。 Y、X1、X2という３つの変数があって、それらの組合せによって、３つの相関係数があります。 Yが目的変数、X1、X2が説明変数です。

この条件式が成り立っている場合、重回帰分析と単回帰分析で、X1の係数の符号（プラスとマイナス）が反対になります。

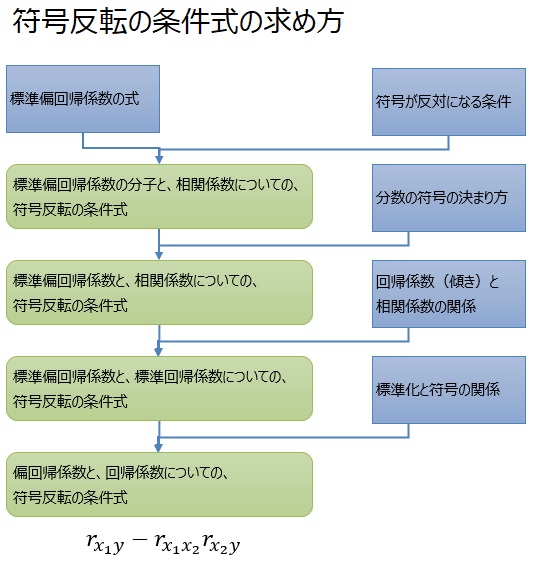
符号反転の条件式の求め方

符号反転の条件式は、複数の知識の組み合わせでできています。以下では、それらの知識をひとつずつ説明します。最終的に、符号反転の条件式に行き着きます。
符号反転の条件式の求め方

Y、X1、X2という３個の変数について、「Y = A1 * X1 + A2 * X2 + B」という重回帰分析を考えます。

A1は、「偏回帰係数」と言います。 Y、X1、X2が標準化されている時は、「標準偏回帰係数」と言います。ここでは、「A1'」と書くことにします。

標準偏回帰係数のページにあるように、A1'を求める式は、以下になります。
符号反転

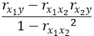
変数が３個あると、相関係数の組合せは３種類ありますが、A1'は、３種類全部が入っている式になっています。

例えば、「0.7」という数字があったとします。これは、正（プラス）の数です。

「P = Q - s」という式があり、「Q = 0.7」とします。この時に、Pが負（マイナス）の数になるための条件は、「0.7 < s」です。

この例を一般化すると、「Qが正の時、PとQの符号が反対になる条件は、Q < s」です。

次に、例として、「P = Q - s」という式があり、「Q = -0.6」とします。この時に、Pが正（プラス）の数になるための条件は、「-0.6 > s」です。

この例を一般化すると、「Qが負の時、PとQの符号が反対になる条件は、Q > s」です。

A1'の分子は、以下になっています。 YとX1の相関係数が入っています。
符号反転

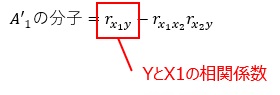
YとX1の相関係数が正の場合、 A1'の分子と、YとX1の相関係数の符号が反対になる条件は、上記の考え方を使うと、以下になります。
符号反転

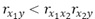
YとX1の相関係数が負の場合は、不等号の向きが逆になります。

この式は、単回帰分析と重回帰分析で、X1の符号が反転するための条件式と同じですが、ここまでの説明では、A1'の分子と、YとX1の相関係数の符号が反対になるための条件式です。以下では、この条件式が、なぜ、X1の符号が反転するための条件式になるのかを説明します。

「4 / 5」という分数があったとします。分子と分母の両方が正なので、この数字は、正です。

「(-4) / 5」という分数があったとします。分子が負、分母が正なので、この数字は、負です。

分母が正の場合、分子の符号が、その分数の符号と同じになります。

A1'は、分母が以下のようになっています。
符号反転

A1'の分母は、必ず正になります。そのため、A1'の符号は、分子の符号次第ということになります。

このことから、「A1'の分子と、YとX1の相関係数の符号が反対になるための条件式」は、「A1'と、YとX1の相関係数の符号が反対になるための条件式」と、読み替えることができます。

単回帰分析をすると、「Y = a1 * X1 + b」という式を作れますが、a1の方は「回帰係数」や「傾き」と呼ばれます。

傾きと相関係数と標準化のページにもありますが、YとX1が標準化されている時の回帰係数をa1'と書くと、a1'と、YとX1の相関係数が同じものになります。
符号反転

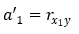
このことから、「A1'と、YとX1の相関係数の符号が反対になるための条件式」は、「A1'と、a1'の符号が反対になるための条件式」と、読み替えることができます。

上記の話は、Y、X1、X2が標準化されていることを前提にして、「A1'と、a1'の符号が反対になるための条件式」を求めています。

標準化は、スケールを変換する処理なので、標準化の有無で、係数の符号は変わりません。よって、この条件式は、「A1と、a1の符号が反対になるための条件式」になります。

つまり、以下の式は、「単回帰分析と重回帰分析で、X1の符号が反転するための条件式」ということになります。
符号反転

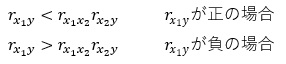
以上で、符号反転の条件式が求まりました。

「パラドックスで学ぶ統計学」岩崎学・川崎玉恵　著　共立出版　2025
第７章と第８章で、符号反転の条件式を導出しています。
ちなみに、筆者は、この本に書いてあることを知らずに自分で導き、後になって、この本に書いてあるのを見つけました。