 僩僢僾儁乕僕 |
傂偲偮忋偺儁乕僕 |
栚師儁乕僕 |
偙偺僒僀僩偵偮偄偰 | ENGLISH
僩僢僾儁乕僕 |
傂偲偮忋偺儁乕僕 |
栚師儁乕僕 |
偙偺僒僀僩偵偮偄偰 | ENGLISH
 僩僢僾儁乕僕 |
傂偲偮忋偺儁乕僕 |
栚師儁乕僕 |
偙偺僒僀僩偵偮偄偰 | ENGLISH
僩僢僾儁乕僕 |
傂偲偮忋偺儁乕僕 |
栚師儁乕僕 |
偙偺僒僀僩偵偮偄偰 | ENGLISH
晞崋斀揮 偺儁乕僕偱偼丄晞崋斀揮偺椺偺傂偲偮傪愢柧偟偰偄傑偡丅
偙偺儁乕僕偱偼丄偦偺懠偺椺傪愢柧偟傑偡丅
昅幰偼丄偳偺傛偆側僨乕僞偺応崌偵晞崋斀揮偑婲偒傞偺偐傪丄偱偒傞偩偗栐梾揑偵挷傋偰傒傑偟偨丅 MECE側暘愅 偱偡丅 挷傋偨傕偺傪懱宯揑偵惍棟偟偨傜丄12僷僞乕儞偁傝傑偟偨丅
12僷僞乕儞偼丄廳夞婣暘愅傪偡傞帪偵丄曄悢娫偺帩偭偰偄傞娭學傪暘椶偟偨傕偺偱偡丅
12僷僞乕儞偱偁傞偐偳偆偐偲丄晞崋斀揮偑婲偒傞偐偳偆偐偼丄柍娭學偱偡丅
偦偺僷僞乕儞偵側傟偽丄昁偢晞崋斀揮偑婲偒傞偺偱偼側偔丄晞崋斀揮偑婲偒傞忦審偵側偭偰偄傞偲婲偒傑偡丅
晞崋斀揮偑婲偒傞忦審偼丄
晞崋斀揮
偺儁乕僕偱愢柧偟偰偄傑偡丅
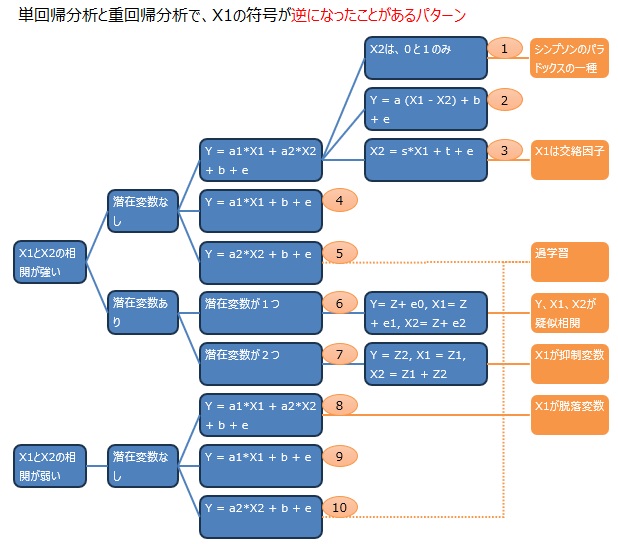
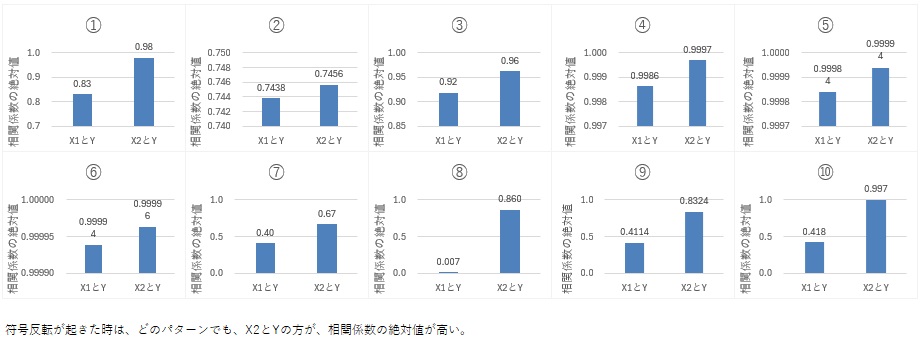
悽偺拞偺夝愢偱偼丄愢柧曄悢娫偵憡娭偑偁傞応崌傪丄晞崋斀揮偑婲偒傞椺偲偟偰愢柧偡傞偙偲偑懡偄偱偡丅
埲壓偺丄嘆偐傜嘒偼丄愢柧曄悢娫偺憡娭偑嫮偄応崌傪嵶偐偔暘偗偰偄傑偡丅
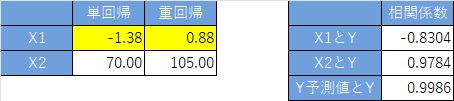
偙偺僨乕僞偼丄埲壓偺幃傪巊偭偰丄嶌偭偰偄傑偡丅 X2偼侽偲侾偟偐側偔丄擇抣偵側偭偰偄傑偡丅
偙偺椺偼丄僔儞僾僜儞偺僷儔僪僢僋僗偺堦庬偱偡丅
X1偲Y偺僌儔僼傪尒傞偲丄俇屄偺僒儞僾儖慡懱偱偼丄晧偺憡娭偵側偭偰偄傞偺偱偡偑丄X2偺抣偱僌儖乕僾暘偗偡傞偲丄僌儖乕僾偺拞偱偼丄惓偺憡娭偵側偭偰偄傑偡丅
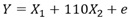
乽Y梊應抣乿偼丄X1偲X2偺椉曽傪愢柧曄悢偵偟偨廳夞婣暘愅偱悇掕偟偨抣偱偡丅
Y偲Y梊應抣偑捈慄揑偵暲傇偲丄惛搙偑崅偄偙偲傪堄枴偟偰偄傑偡丅
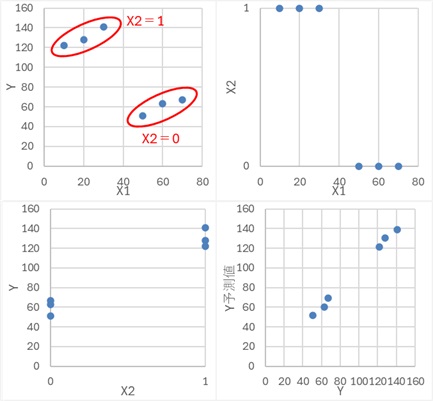
廳夞婣暘愅偺學悢偼丄僨乕僞偺惗惉幃偲傎傏摨偠抣偑媮傑偭偰偄傑偡丅
偙偺僨乕僞偼丄埲壓偺幃傪巊偭偰丄嶌偭偰偄傑偡丅
X1偲X2偵憡娭偑偁傞拞偱丄X1偲X2偺嵎傪庢傞偲丄X1丄X2偵嫟捠偟偨摿挜埲奜偑拪弌偝傟傑偡丅
偦傟偲丄Y偑憡娭偟偰偄傞僷僞乕儞偱偡丅
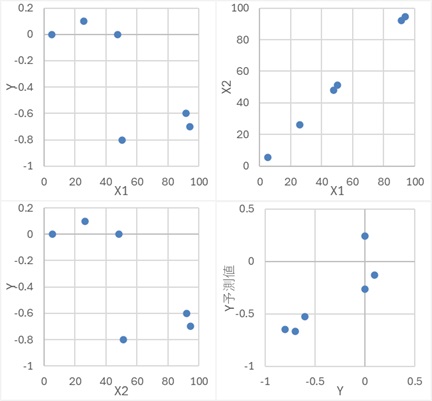

偙偺僨乕僞偼丄埲壓偺幃傪巊偭偰丄嶌偭偰偄傑偡丅
X1偑丄Y偲X2偺椉曽偺愢柧曄悢偵側偭偰偄傑偡丅
X1偼丄摑寁揑場壥悇榑偱丄乽岎棈場巕乿偲屇偽傟傑偡丅
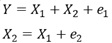
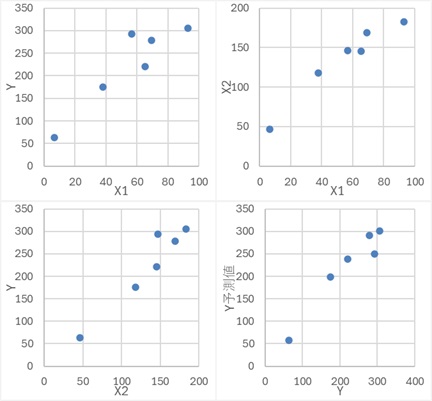

偙偺僨乕僞偼丄埲壓偺幃傪巊偭偰丄嶌偭偰偄傑偡丅
X1偲X2偼丄Z偲偄偆曄悢偐傜嶌傜傟偰偄傞揰偑嫟捠偟偰偄偰丄媈帡憡娭偺娭學偱偡丅
Y偼丄X1偐傜嶌傜傟偰偄偰丄X2偲偼柍娭學偱偡丅
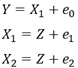
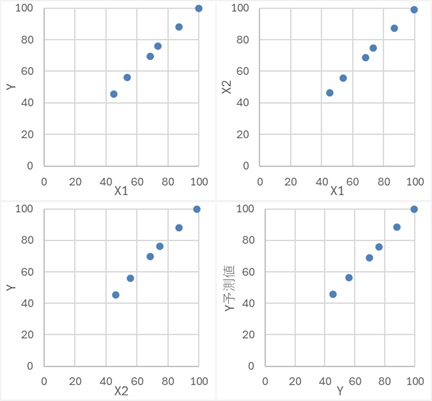
Y偼X1偐傜嶌傜傟偨僨乕僞偩偲偟偰傕丄X2偺曽偑Y偲憡娭偑嫮偄偺側傜丄廳夞婣暘愅偺學悢偵晞崋斀揮偑婲偒傑偡丅

晛捠偼丄Y偑X1偐傜嶌傜傟偰偄傞偺側傜丄Y偲憡娭偑嫮偄偺偼丄X1偱偡丅 偟偐偟丄X1偲X2偺憡娭偑嫮偄応崌偼丄X1偲X2偑帡偰偄傞偺偱丄X2偺曽偑丄Y偲偺憡娭偑嫮偔側偭偰偄傞偙偲偑偁傝傑偡丅 晞崋斀揮偑婲偒偨偺偼丄偦偺傛偆側帪偱偡丅
偙偺僨乕僞偼丄埲壓偺幃傪巊偭偰丄嶌偭偰偄傑偡丅
X1偲X2偼丄Z偲偄偆曄悢偐傜嶌傜傟偰偄傞揰偑嫟捠偟偰偄偰丄媈帡憡娭偺娭學偱偡丅
Y偼丄X2偐傜嶌傜傟偰偄偰丄X1偲偼柍娭學偱偡丅
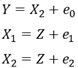
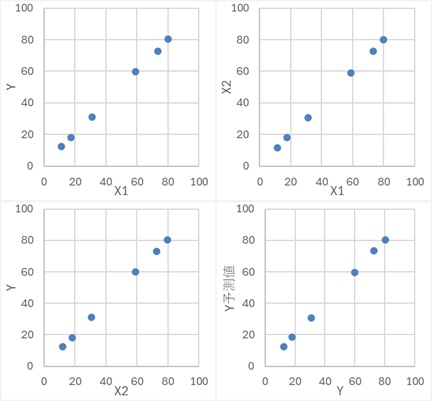
Y偑X2偐傜嶌傜傟偨僨乕僞側偙偲傕偁傝丄X2偺曽偑Y偲憡娭偑崅偄偱偡丅X1偵晞崋斀揮偑婲偒傑偡丅
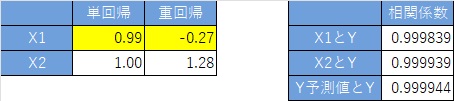
栚揑曄悢偲愢柧曄悢偑丄傕偲傕偲柍娭學偺応崌偱偡丅
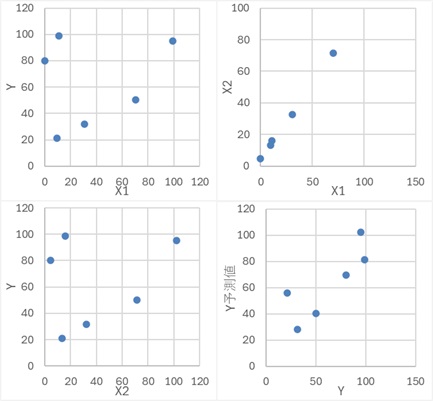
偙偺僷僞乕儞偺応崌丄扨夞婣暘愅偱傕廳夞婣暘愅偱傕丄儌僨儖偑崌偭偰偄側偄偺偱偡偑丄僨乕僞偩偗傪尒偰偄傞偲丄偦傟偑傢偐傜側偄偙偲偑偁傝傑偡丅
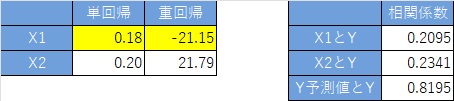
偙偺僨乕僞偼丄埲壓偺幃傪巊偭偰丄嶌偭偰偄傑偡丅
Y丄X1丄X2偵偼丄捈慄揑側娭學偼側偄偺偱偡偑丄Z偑嫟捠偵側偭偰偄傞偺偱媈帡憡娭偺娭學偑偁傝傑偡丅
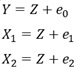
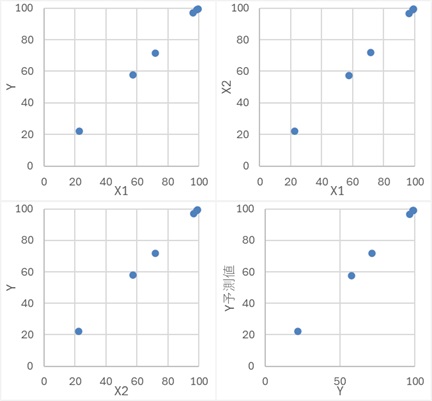

偙偺僨乕僞偼丄埲壓偺幃傪巊偭偰丄嶌偭偰偄傑偡丅 Z1丄Z2偲偄偆曄悢偑偁傝傑偡丅 Y偼丄Z2偺堦師娭悢偱丄X1偼Z1偺娭悢側偺偱丄Y偲X1偵偼捈愙揑側娭學偼側偄偱偡丅
Y偲X2偱扨夞婣暘愅傪偡傞偲丄X2偵娷傑傟偰偄傞Z1偑僲僀僘偵側傝傑偡丅
偦偙偱丄Z1傪帩偭偰偄傞X1傕壛偊偨廳夞婣暘愅偵偡傞偲丄惛搙偑忋偑傝傑偡丅
偙偺傛偆側X1偼丄乽梷惂曄悢乮Suppressor Variable乯乿偲屇偽傟傑偡丅
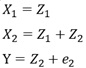
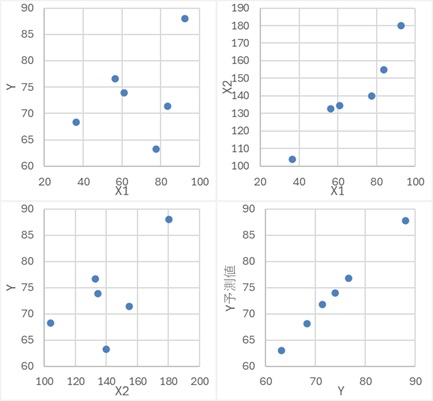

側偍丄嘕偺僷僞乕儞偺傛偆偵丄愢柧曄悢娫偺憡娭偑庛偔丄Y偼丄X2偺堦師娭悢偺応崌偱傕丄晞崋偺斀揮偼婲偒傑偡丅
乽X2扨撈偺扨夞婣暘愅傛傝傕丄X1傪壛偊偨廳夞婣暘愅偺曽偑憡娭學悢偺愨懳抣偑戝偒偄乿傗丄乽晞崋偑斀揮偡傞乿偲偄偆偙偲偱偼丄梷惂曄悢偐偳偆偐偼傢偐傜側偄偱偡丅 X1偲X2偺憡娭偺嫮偝偐傜悇應偡傞昁梫偑偁傝傑偡丅
悽偺拞偺夝愢偱偼丄愢柧曄悢娫偵憡娭偑偁傞応崌傪丄晞崋斀揮偑婲偒傞椺偲偟偰愢柧偡傞偙偲偑懡偄偱偡偑丄 愢柧曄悢娫偺憡娭偑庛偔偰傕丄晞崋斀揮偼婲偒傑偡丅
嘓偐傜嘖偼丄愢柧曄悢娫偺憡娭偑庛偔偰傕丄晞崋斀揮偑婲偒傞働乕僗偱偡丅
偙偺僨乕僞偼丄埲壓偺幃傪巊偭偰丄嶌偭偰偄傑偡丅
愢柧曄悢娫偵憡娭偑側偔丄Y偼X1偲X2偺慄宍榓偱偱偒偰偄傞僷僞乕儞偱偡丅
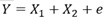
Y偼丄X1偲X2偺慄宍榓側偺偵丄曅曽偩偗偱夞婣暘愅傪偟偰偄傞帪偼丄敳偗棊偪偨曽偑乽扙棊曄悢乿偲屇偽傟傑偡丅 敳偗棊偪偨偙偲偵傛偭偰婲偙傞岆夝偼丄乽扙棊曄悢僶僀傾僗乿偲屇偽傟傑偡丅
偙偺僨乕僞偵懳偟偰丄X1偲Y偵傛傞扨夞婣暘愅偡傞偲丄X2偑敳偗偨偙偲偵側傝傑偡丅
偙偺応崌偼丄杮棃偼僾儔僗偵側傞偼偢偺晞崋偑丄儅僀僫僗偵側偭偰偄傑偡丅

偙偺僨乕僞偼丄埲壓偺幃傪巊偭偰丄嶌偭偰偄傑偡丅
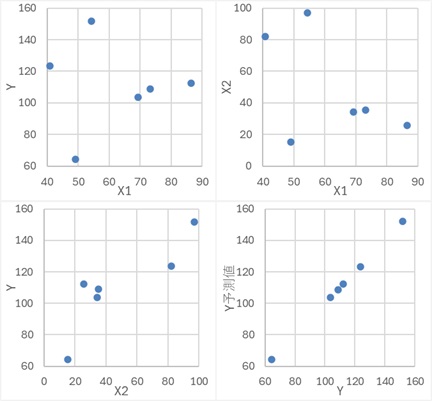
Y偼丄X1偐傜嶌傜傟偰偄偰丄X2偲偼柍娭學偱偡丅
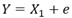
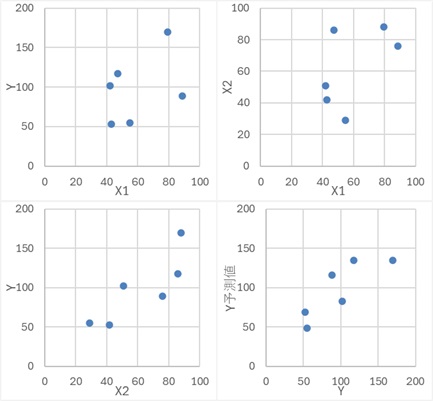
Y偼X1偐傜嶌傜傟偨僨乕僞偩偲偟偰傕丄X2偺曽偑Y偲憡娭偑嫮偄偺側傜丄廳夞婣暘愅偺學悢偵晞崋斀揮偑婲偒傑偡丅

晛捠偼丄Y偑X1偐傜嶌傜傟偰偄傞偺側傜丄Y偲憡娭偑嫮偄偺偼丄X1偱偡丅 偟偐偟丄乽Y偑X1偐傜嶌傜傟偰偄傞乿偲側偭偰偄偰傕丄Y偲X1偺憡娭偑嫮偔側偄応崌偼丄柍娭學側X2偺曽偑丄Y偲偺憡娭偑嫮偔側偭偰偄傞偙偲偑偁傝傑偡丅 晞崋斀揮偑婲偒偨偺偼丄偦偺傛偆側帪偱偡丅
愢柧曄悢娫偵憡娭偑側偔丄Y偼X2偺堦師娭悢偱偱偒偰偄傞僷僞乕儞偱偡丅
偙偺僨乕僞偼丄埲壓偺幃傪巊偭偰丄嶌偭偰偄傑偡丅
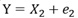
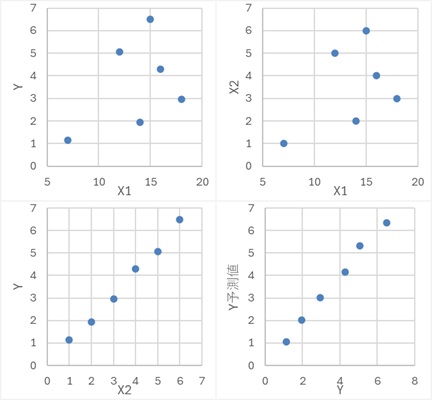
偙偺僷僞乕儞偺応崌丄廳夞婣暘愅偺儌僨儖偼晄惓夝偱丄Y偲X2偺扨夞婣暘愅偺儌僨儖偑惓夝偵側傞偺偱偡偑丄
Y梊應抣偲Y偺憡娭學悢偺曽偑丄X2偲Y偺憡娭學悢傛傝傕戝偒偄偨傔丄乽廳夞婣暘愅偺曽偑椙偄乿偲偄偆娫堘偭偨敾抐傪偟偑偪偱偡丅

偙傟偼丄夁妛廗偺椺偱偡丅 傑偭偨偔娭學偺側偄曄悢偩偲偟偰傕丄儌僨儖偵壛傢傞偲丄Y梊應抣偲Y偺憡娭學悢偼忋偑傞偺偱丄憡娭學悢偑崅偔側偭偨偙偲偩偗偱偼丄儌僨儖偺懨摉惈傪敾抐偟偰偼偄偗側偄偱偡丅
俁偮偺曄悢偑丄偍屳偄偵柍娭學偺応崌偱偡丅
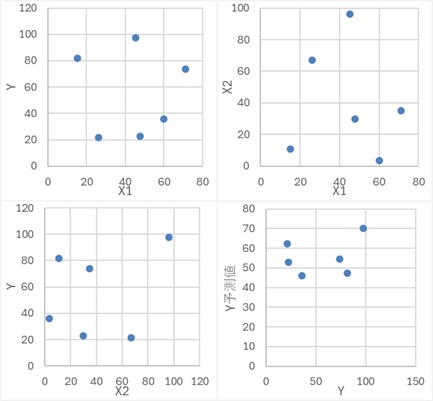
偙偺僷僞乕儞偺応崌丄扨夞婣暘愅偱傕廳夞婣暘愅偱傕丄儌僨儖偑崌偭偰偄側偄偺偱偡偑丄僨乕僞偩偗傪尒偰偄傞偲丄偦傟偑傢偐傜側偄偙偲偑偁傝傑偡丅

弴楬


 師偼
晞崋斀揮偲僒儞僾儖悢
師偼
晞崋斀揮偲僒儞僾儖悢

