トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
符号反転の事例集 は、どれもサンプル数が６個の場合です。
このページでは、「サンプル数が多い場合に、符号反転がどうなるのか？」 具体的には、「符号反転が起きるのは、サンプル数が少ない時だけでは？」、 「同じサンプル数でも、パターンによって、符号反転の発生率が変わるのでは？」という疑問について、調べたことを説明します。
このページでは、以下ようなグラフを、パターン別に作っています。
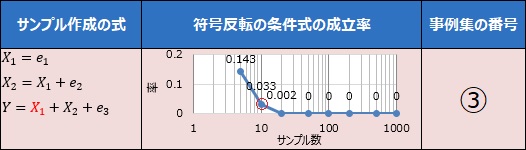
まず、左側に、データを作成する時の式があります。 この例の場合は、X1が乱数、X2は、X1に乱数を足したもの、YはX1とX2の和に、さらに乱数を足したものであることを表しています。
ここで使用した乱数は、0から1までの、一様分布に従う乱数です。 e1、e2、e3とは、それぞれ異なることを表しています。
グラフの横軸はサンプル数です。 赤丸をしたところは、「10」ですが、10個のサンプル数で相関係数を計算していることを表しています。
サンプル数が10の時は、10個のサンプルを1000回発生しています。 毎回、X1とX2、X1とY、X2とYの、それぞれの組合せについて、相関係数を計算します。 そして、符号反転の条件式に当てはまれば「1」、当てはまらなければ「0」とします。
1000回分を集計すると、条件式に当てはまる確率が求まります。 この作業を、サンプル数を5から1000まで、段階的に変えて実施して作ることで、グラフを作っています。
この例の場合は、まず、サンプル数が5個の時、成立率が0.143で、10個の時、0.033です。 「符号反転は、まれに起きる」ということがわかります。 次に、サンプル数が20個以上の場合は、符号反転が起きないこともわかります。
符号反転の事例集 のパターンのついて、系統的に調べてみた結果、以下のようにまとめられることがわかりました。
明確に分かれました。
パターンは12種類ですが、符号反転の表れ方は、３種類に分かれています。
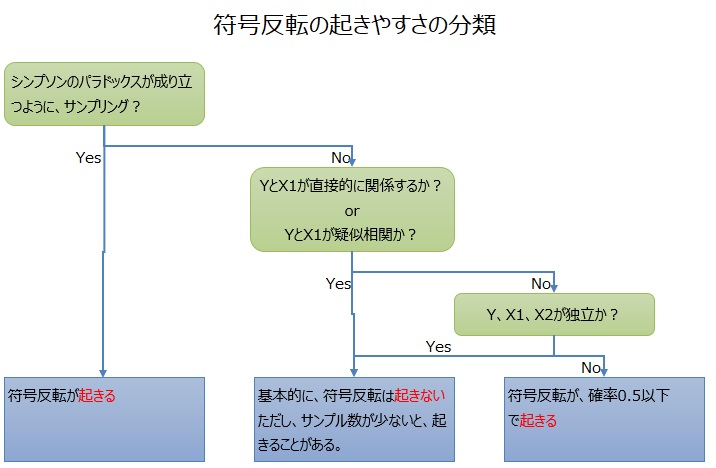
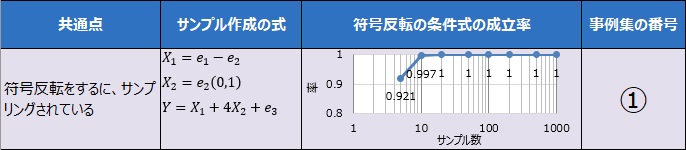
シンプソンのパラドックスが成り立つパターンの時は、質的変数で層別した時の傾きと、全体的な傾きの符号が逆になるようにサンプリングしています。
符号反転は、必ず起きます。
ただし、このシミュレーションのように、ランダムにばらつくようにすると、サンプル数が少ない時に、符号が逆になっていないことがあります。
「基本的に、符号反転は起きない。例外的に、サンプル数が少ない時は、符号反転が起きる事がある」となったパターンです。
符号反転の事例集 の例は、サンプル数が少ないので、様々なパターンで符号反転が起きる事例を見つけていますが、サンプル数が多いと、結果が変わることを推察できます。
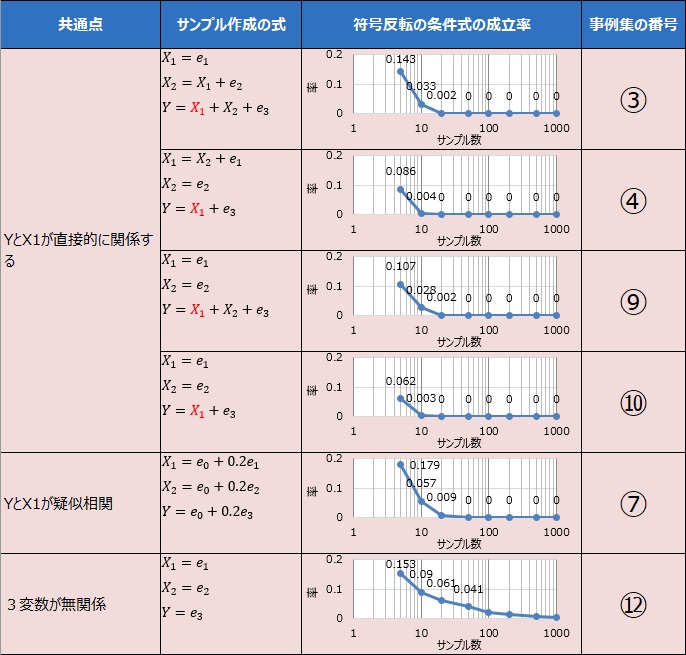
このパターンは、大きく分けて、上の５個と、最後の１個に分かれます。 上の５個の中の４個は、YとX1が直接的に関係している場合です。 １個は、YとX1が疑似相関の関係の時です。 いずれにしても、YとX1には、関係があります。
③、④、⑨、⑩については、YとX1の相関が高いことで、下の式の、赤枠で囲った部分の数字が大きくなり、条件式が成立しにくくなったことが理由と考えられます。
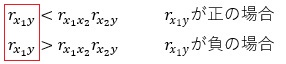
⑦については、３つの変数で作られる３つの相関係数が、すべて高くなります。 例えば、３つの相関係数がすべて0.9だった場合、条件式の左辺側が0.9、右辺側が0.81になります。 このため、条件式が成立しにくくなったことが理由と考えられます。
⑫は、⑦の逆で、３つの変数で作られる３つの相関係数が、すべて低くなります。 例えば、３つの相関係数がすべて0.1だった場合、条件式の左辺側が0.1、右辺側が0.01になります。 このため、条件式が成立しにくくなったことが理由と考えられます。
「基本的に符号反転は起きる。確率は0.5くらい」となったパターンです。 ⑪だけ、0.2と0.3の間ですが、それ以外は、0.5くらいになっています。
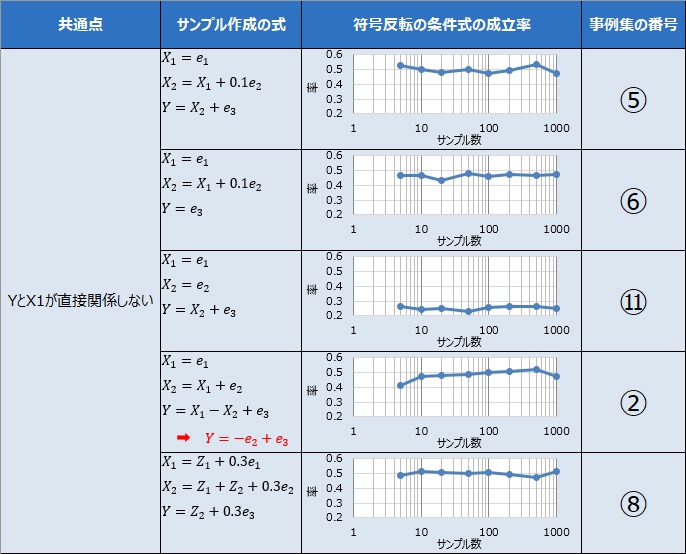
⑤と⑥については、X1とX2の相関が高いことで、下の式の、赤枠で囲った部分の数字が１に近くなり、条件式が成立しやすくなったことが理由と考えられます。
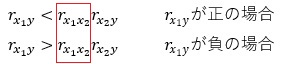
⑪については、YとX2の相関が高いことで、下の式の、赤枠で囲った部分の数字が１に近くなり、条件式が成立しやすくなったことが理由と考えられます。
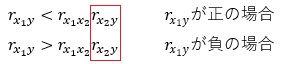
②、⑧については、YとX1の相関が低いことで、下の式の、赤枠で囲った部分の数字が０に近くなり、条件式が成立しやすくなったことが理由と考えられます。
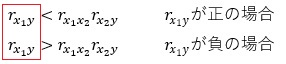
共通する理由として、この分類になったものは、X1と直接関係していないことがわかります。 YとX2が直接関係していて、X2はX1と直接関係しているのなら、間接的には関係していることになりますが、そうなっていても、符号反転が起きやすくはなっていないことがわかります。
なお、YとX1が直接関係しないことに加えて、３変数がお互いに無関係な場合に限っては、この分類には入らず、ひとつ前の分類になっています。
符号反転について、「特殊な現象が起きている」と解釈した研究が、かなりあるようです。
このページの調査結果から考えると、シンプソンのパラドックスが成り立っている場合を除いて、符号反転は「必ず起きる」という性質のある現象ではないです。 データを取ったタイミングによって、起きたり起きなかったりする性質があります。
特に、YとX1に関係がない時は、0.5の確率で発生します。 無関係な変数に対して、「何か特別な性質を持った変数」という仮説を立てても、その先には何もないのではないかと考えています。
このページの調査は、モデル式を作って、モデル式から生まれる1000セットの結果を見ることで、符号反転の表れ方を見ています。 現実のデータ分析では、1000セットの中の１セットを、現実のデータとして手に入れて、それを分析することになります。 １セットだけからわかることにこだわると、現象を解明する方向性としては、良くないようです。
順路
次は
多重共線性
