o値の計算方法は、大きく４つのタイプがあります。
目的に合う手法を模索して作って行く中で、10種類くらい作ってみたら、４つのタイプに分かれることに気付きました。
以下は、それぞれの検定に対して、考案したo値の計算方法の対応です。
それぞれのページでは、計算方法による違いがあります。
例えば、
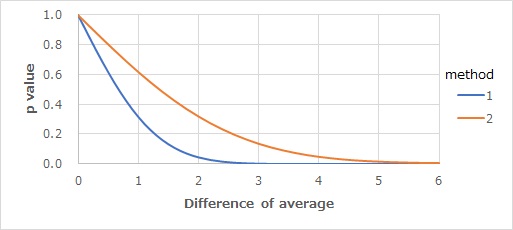
平均値の差の検定のo値
には、下のグラフがあります。
相関係数の２乗は、「寄与率」としての数学的な意味があります。
相関係数は、２つの連続変数の関係の指標として知られていますが、「０と１」という数字にすれば、２値変数でも使えます。これを応用します。
o値Bというのは、 21世紀の検定 として筆者が考案したもののうち、z検定の応用でo値を計算する方法です。
手順としては、まず、nの平方根と似た値を、z検定の検定統計量にかけます。 これによって、検定統計量の分母が、標準誤差から標準偏差に変わります。 次に、計算された確率の値を２倍します。 この手順は、p値の計算では、片側検定から両側検定への変換で使いますが、o値の計算では、０から１の範囲で変化する指標にするために２倍します。
式の違いはシンプルですが、式の意味は違います。
t値やz値といった検定統計量は、 標準化 によって作られる指標です。 分母が 標準誤差 になっています。 この検定統計量からp値が求まります。
o値は、p値の計算式の分母を、標準誤差から標準偏差に変更することで求めることができます。 この発想で求めたo値は、本サイトでは、「Aタイプ」と呼んでいます。
Aタイプは、従来から使われて来たソフトを転用できるので、導入がしやすいです。
z検定では、標準正規分布を仮定して、検定統計量がどの位置に来るのかを調べます。
例えば、検定統計量が「2」なら、p値は、0.025（2.5%）になります。
平均値の検定をする時は、分布は平均値の分布です。0かどうかを調べる場合（帰無仮説が、「平均値＝0」の場合）は、 0を中心とした分布に対して、実際のデータから計算された平均値が、どの位置に来るのかを調べます。 平均値の分布に対して、ある平均値の現れやすさを調べます。
p値は、その位置よりも外側の面積の、全体からの割合です。
o値の計算では、標準誤差から標準偏差に変わったので、データの分布に対してどうなのかを調べています。
平均値は、本来なら、データの中心にあるはずですが、計算した平均値が中心からどのくらい離れているのかを調べます。 その離れ具合を、面積の割合で表現しています。
p値は、平均値の分布に対しての、ある平均値の位置から求める割合なので、「確率」としての意味を持っています。
一方、o値については、「割合」ではありますが、「確率」としての意味は持っていないです。 確率ではないのですが、確率のような感覚で使える指標として作られています。
Cタイプは、2つのグループを比較する時に、2つのグループの分布を重ね合わせて、重なり具合の割合をo値として決めた指標です。
Dタイプは、ノンパラメトリックな方法です。
順路
次は
21世紀の、相関係数の検定
