発生数の差の検定

このページの名前は、「発生数の差の検定」にしましたが、一般的ではないです。

「欠点数の差の検定」、「不適合数の差の検定」という名前だと、参考文献が見つかります。ただ、「欠点数」や「不適合数」というのは、品質学の分野の言葉なので、それ以外の分野の人には、わかりにくさになっています。

発生数のデータについての分析方法です。

発生数とは

発生数というのは、発生回数や生起回数とも呼ばれます。

より正確には、単位時間内、１個当たりなど、何らかの範囲の中での、発生数のことです。

発生数を目的変数Yにする回帰分析として、ポアソン回帰分析があります。

発生数の差の検定も、ポアソン分布を元にした検定になります。

それぞれのサンプルについて、０と１に相当するものしかない場合、比率の差の検定になります。

発生数の検定は、それぞれのサンプルについて、０以上の整数のデータがある場合です。

例えば、「発生数が10以上は、不良品」というルールがあると、発生数のデータは、比率のデータに変換できます。

そのため、工場のデータ分析では、同じデータに対して、比率で考える場合と、発生数で考える場合の、２つの見方ができます。

分散の比の検定は分散の比が従うF分布を直接使う、F検定が開発されています。

発生数の差の検定については、ポアソン分布を直接使う方法は、世の中にないようです。ポアソン分布は、期待値について、平均値がλ、分散がλになるので、それらを使って、下記のz値を求め、z検定をします。

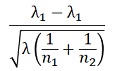
分母のλは、全体の平均の発生数です。

筆者の調べた限りでは、発生数の差の検定については、効果量を示している文献はないようです。

平均値の差の検定の効果量は、平均値の差を、標準偏差で割る形なので、同様に考えれば、発生数の差の検定の効果量は、下記が良いと考えられます。

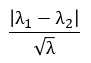
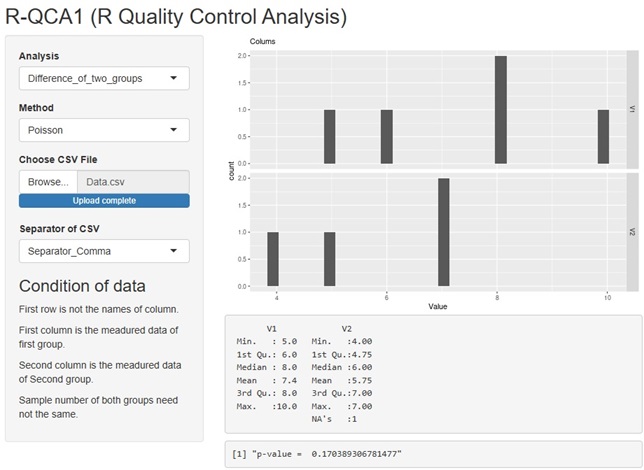
Rの実施例は、 Rによる違いの有無の分析のページにあります。

Rがインストールされていないパソコンやタブレットなど、手軽にやるには、 R-QCA1 が良いかと思います。
ウェブアプリ　R-QCA1

「2つの母不適合数の差の検定を例題で解説　～統計的検定（その10）～」　QCとらのまき
「2つの母不適合数の差の検定」という名前で紹介しています。
https://qctoranomaki.com/sqc/statistical-testing/step10/