RMSE（Root Mean Squared Error：二乗平均平方根誤差）

RMSE
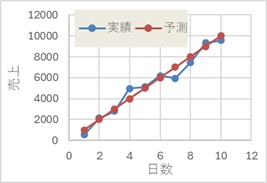
上のグラフは、売上の予測と実績を表しています。予測は、直線を仮定して計算しています。

予測の精度は、予測値からの実績のばらつきの大きさを表すものになりますが、標準偏差では測れないです。このような場合に、標準偏差のようにして使えるのが、RMSE（Root Mean Squared Error：二乗平均平方根誤差）です。

RMSEの式

RMSEは、誤差の二乗平均の平方根です。その差を二乗した値の合計をデータの個数で割って、平方根を計算すると、RMSEになります。
RMSE

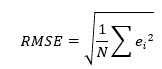
具体的な計算例は、下記になります。
RMSE

RMSEは、あまり知られていませんが、最小二乗法は、回帰分析の解法としてよく知られています。

RMSEが最小になるように、モデルの係数を最適化するのが、最小二乗法です。

上の例のようなデータについて、直線からのばらつきを測る尺度としては、相関係数があります。

RMSEは、誤差から計算するので、直線ではないモデルでも、測れるところが違います。

また、予測値を区間推定する用途でも使えます。

相関係数は、-1から1の範囲の尺度です。

一方、RMSEは、データの単位を持っています。例えば、上の例の場合は、RMSEが542.4ですが、この範囲がいわゆる標準偏差の一倍に相当するので、中心値から±542.2円の範囲に、全体の約70%が入ることを意味しています。

RMSEは、データの範囲のどこをとっても、等分散なことを仮定しています。

等分散ではない場合に、RMSEで最適化をすると、分散の大きな領域に偏った最適化になって、良くありません。

「等分散ではない」といってもいくつか種類がありますが、このサイトでは、以下のページで扱っています。

順路