等分散
というのは、横軸がいくつになっても縦軸のばらつき方が一定な事です。
等分散な場合、回帰分析で、傾きの効果を差し引いて、ばらつきだけのグラフにすると、下のようになっています。
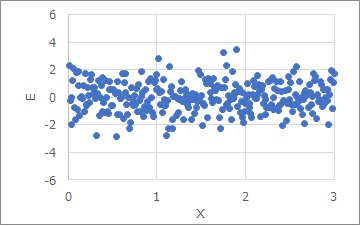
世の中の解説では、「回帰分析は、等分散を前提とした理論です。等分散ではないデータを扱うのは適切ではありません。」という説明がされることがありますが、 等分散ではない時に、どのようにすれば良いのかはあまり説明されません。
説明される場合は、 分野によりますが、生物関係では、 一般化線形モデルが紹介されることがあります。 計量経済学 では、加重最小二乗法が紹介されます。
世の中で解説されることはないようなのですが、 比例分散の回帰分析 も等分散ではない回帰分析です。 「等分散ではない」というだけだと、様々なパターンがありそうですが、「等分散ではない」の多くの場合で、比例分散になっていることはよくあります。 そのため、等分散ではない時に比例分散として扱うのは、選択肢として有望です。
ちなみに、世の中の解説だと等分散の場合が普通なので、比例分散は特殊な分析方法のような説明の仕方になるのですが、 筆者としては、比例分散の方が物理現象としては多くて、等分散の方が少ないような気がしています。 実際、 比例分散への品質工学のアプローチ のように、分野によっては、比例分散が当たり前のように出て来ることもあります。
なお、一般化線形モデルで扱える非等分散と、比例分散が扱える非等分散は違います。 一般化線形モデルでは、正規分布以外の時に非等分散が扱えるようになりますが、比例分散では、正規分布でも非等分散が扱えます。
比例分散の回帰分析 のポイントは、YをXで割ったY/Xを分析していく点になっています。
比例分散は、分散がXに比例していくことを扱う方法なので、Y/Xがどのような分布をしているのかは、もともと無関係です。 比例分散の回帰分析 のページでは、正規分布と一様分布の場合を紹介していますが、他の分布でも扱えます。
ビッグデータの統計学 のページに、統計学はパソコンや電卓がなかった時代から作られた理論なので、当時は問題にならなかったものの、現代では気にしなければならない問題を紹介しています。
等分散か、比例分散か、という話もそれと似ています。 例えば、n=5だったとしたら、データが直線に乗りそうかどうかは調べられても、「等分散か、比例分散か」といった違いは、グラフを見ても判断ができないです。
順路
次は
比例分散の予測区間
