トップページ |
統計学の解釈学 |
このサイトについて
トップページ |
統計学の解釈学 |
このサイトについて
以下は、筆者の私見です。 誤解があれば、ご教示いただけると幸いです。
このサイトの 時系列近傍法 は、主な使い道が予測です。 それぞれの手法のページで、得意・不得意について説明しています。 実際のところ、どのような違いがあるのかを、このページでは具体例で説明します。
250個のサンプルからできている時系列データを作ります。 1番から200番までのデータでモデルを作り、201番から250番までを予測します。 作成したデータの201番から250番までが、"正解"になるので、どのくらい正解に近いのかを比較します。
比較するのは、以下の手法です。
現実にもありそうなデータを作成して、比較します。
平均が一定のように見えるので、 ホワイトノイズモデル が最適なデータに、他の手法を使った場合の結果です。
RWと移動平均以外は、大差ないです。
ホワイトノイズモデル
とほぼ同じで、平均値の「50」に近い値が出ています。
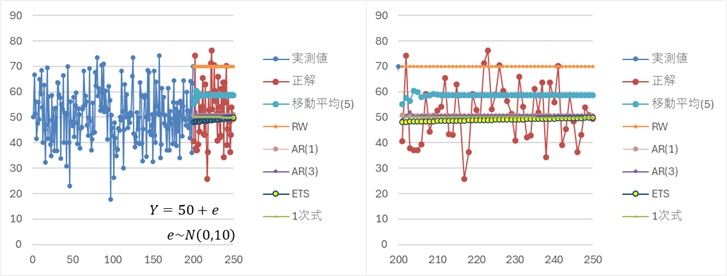
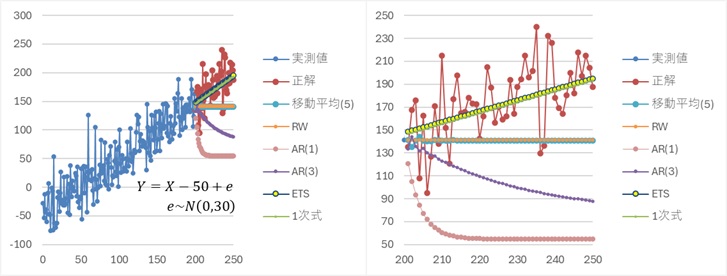
トレンドを予測できているのは、１次式とETSです。
移動平均とRWは、学習データの最後の方の延長として予測しています。
AR(1)とAR(3)は、学習データ全体の平均値に収束しています。
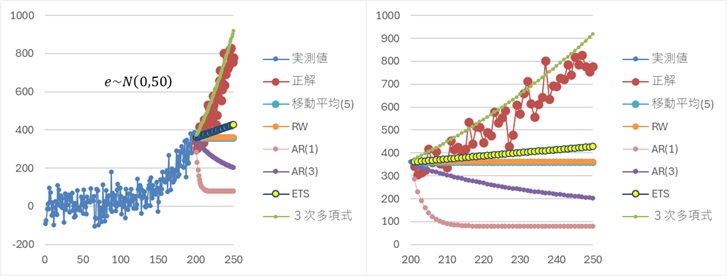
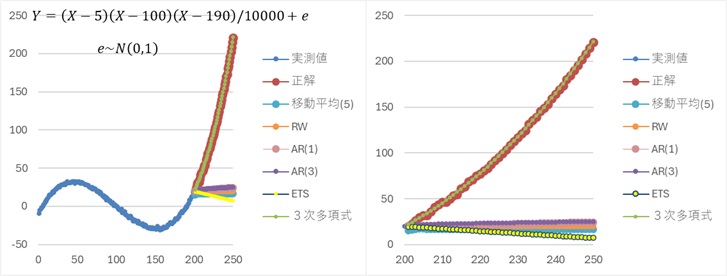
曲線的なトレンドがある場合について、ETSの振る舞いが異なる場合を２例紹介します。 いずれにしても、多項式以外の方法は適していません。
曲線的なトレンドの場合、３次多項式は正解に近い予測をしています。
ETSは、上昇傾向を捉えられているものの、「予測できている」と言えるような感じではありません。
３次多項式だけが、望ましい予測をしています。
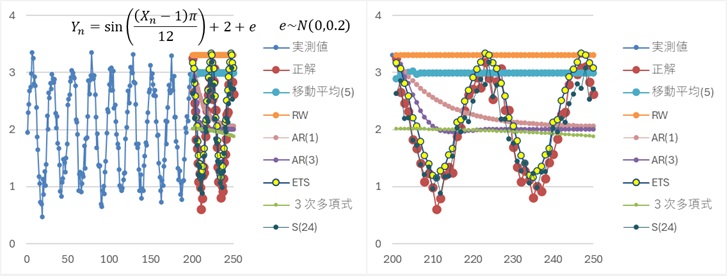
このデータの場合は、周期が24であることがわかっているので、S(24)をSモデルにしています。
ETSとS(24)だけが、周期性を予測できています。
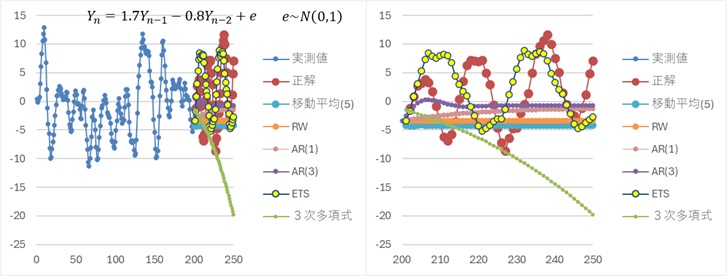
250番目までの予測が、どのモデルでも不可能な場合を２例紹介します。
ある程度は連続性があるので、長期的な予測はできていませんが、201番目くらいの直近の予測なら、そんなに大きくは外していません。
まず、大きく振動していますが、決まった周期は見られない場合です。
周期がわからないので、Sモデルは試していません。
ランダムウォークのような動きの場合です。
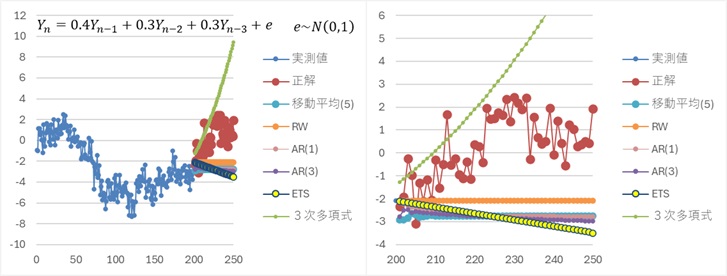
上記では、全体が一定の場合を除いて、移動平均、RW、AR(1)、AR(3)は良いところがありませんでした。
特殊なケースに限られますが、 AR(1)と、AR(3)については、良い予測ができる場合があるので紹介します。
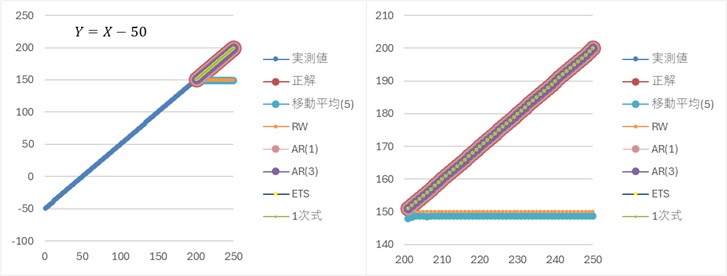
データが直線的に並んでいる場合、上記で紹介したように、ばらつきがある場合は、１次式やETSでないと予測ができません。
しかし、ばらつきがまったくない直線の場合は、AR(1)やAR(3)でも、予測ができます。
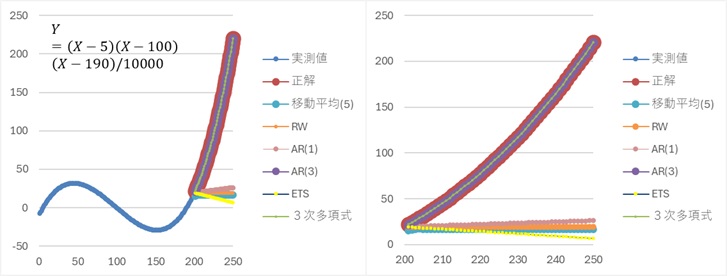
データが３次曲線のように並んでいる場合、上記で紹介したように、ばらつきがある場合は、３次多項式でないと予測ができません。
しかし、ばらつきがまったくない曲線の場合は、AR(3)でも、予測ができます。
データに周期性がある場合、上記では、ETSとSモデルしか、周期性を捉えられませんでした。
しかし、ばらつきがまったくない場合は、AR(3)でも、予測ができます。
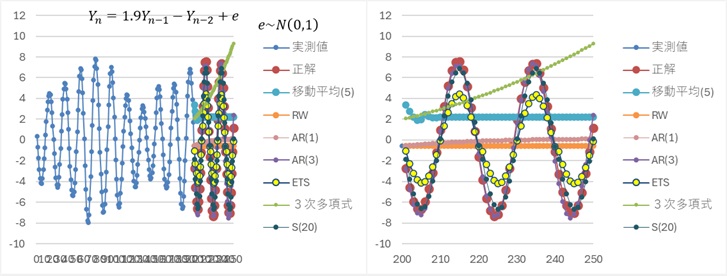
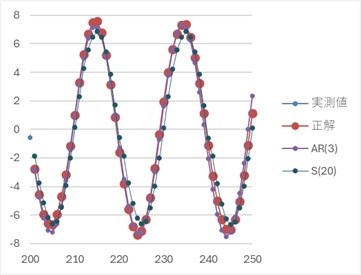
以下は、AR(3)とS(20)だけのグラフです。
AR(3)の方が、S(20)よりも正解に近いです。
