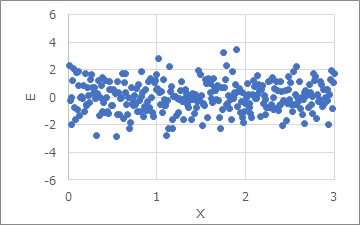
Constant variance means that the variation of the vertical axis is constant no matter how many horizontal axes there are. In the case of equal variance, if you subtract the effect of slope in regression analysis and make a graph of only variation, it is as shown below.

According to the popular commentary, "Regression analysis is a theory that assumes constant variances, and it is not appropriate to deal with data that is not homovariances." It may be explained that, There is not much explanation of how to do it when it is not evenly distributed. If described, Generalized Linear Modelmay be introduced.
Although it does not seem to be explained in the world, regression analysis of proportional variance is also a regression analysis that is not equal variance. If you just say "not equal variance", there are likely to be various patterns, but in many cases of "not equal variance", it is often proportionally distributed. Therefore, treating it as proportional when it is not equal is a proportional option.
By the way, in the explanation of the world, it is normal to use equal variance, so proportional variance is explained as a special analysis method. Personally, I feel that proportional variance is more of a physical phenomenon and less of equal variance. In fact, in some fields, such as Quality Engineering Approach to Proportional variance, proportional variance can be taken for granted.
Note that there is a difference between the non-equal variances that can be handled by generalized linear models and the non-equal variances that proportional variances can handle. Generalized linear models can handle non-uniform variances when they are not normally distributed, while proportional variances can handle non-uniform variances in normal distributions.
The point of regression analysis of proportional variance is to analyze Y/X by dividing Y by X.
Proportional variance is a method that deals with the variance being proportional to X, so the distribution of Y/X is inherently irrelevant. The Regression Analysis of Proportional Variances page introduces the case of normal and uniform distributions, but other distributions can also be handled.
Statistics is a theory that was created in the days when there were no personal computers or calculators, so it was not a problem at the time, but it introduces a problem that we should be concerned about today.
The story of equal distribution or proportional distribution is similar. For example, if n = 5, it is possible to check whether the data is likely to follow a straight line, but it is not possible to judge the difference such as "equal variance or proportional variance" by looking at the graph.
NEXT 

 Prediction interval of Proportional variance
Prediction interval of Proportional variance
