因果関係を分析する場面では、原因と結果の２種類の変数だけで話ができると、「因果関係がある・ない」という結論が楽にできます。
ところが、例えば、「薬を飲んだ人に効果が出ているというが、この薬を飲む人は、他の薬を先に飲んでいることが多い」等、第３の変数の影響を考えないといけないことがあります。
仮説の検証 で議論の中心になることが多いのが、このようなケースです。
２種類のアプローチがあります。
反事実 のデータが何らかの形で取れるのなら、疑似相関の入り込む余地がないので、シンプルに因果関係の有無を検証できるようになります。
ただし、「反事実のデータとみなす」という仮定を使って、このアプローチをする場合は、みなし方がチェックポイントになります。
検証したい説明変数から、他の変数の影響を除去します。 この手順の最初の所で、「介入」という考え方で、式を求めます。 介入すると、第3変数の影響を取り除けますが、これが「d分離」と呼ばれます。
介入として、原因の変数の値が１通りしかない場合を考えます。 すると、これについては、第3変数の影響がないです。 そこから、介入した場合の確率の式を求めます。
明示的に書かれることはないようですが、 統計的因果推論 では、データの種類を整理しておくと良いようです。
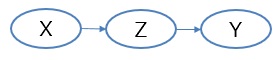
統計的因果推論 では、検証したい変数のZが「薬を飲まない・飲む」というように、二値になっている場合が扱われています 「Z = 0, Z = 1」というような書き方で表すことが多いです。 政治や経済などでは、「その施策に効果があったのか・なかったのか」という判断が必要で、それに合った計算式になっています。
第3変数のXは、検証したい変数に影響しているかもしれない変数ですが、第3変数については、二値ではなく、一般的な量的変数でも扱える理論になっています。
「効果あり・なし」の二値だと、検証の仕方としてはシンプルです。
そこまで明確に結果が出せない場合は、「薬ありで、効果ありになる確率」といった結果の出し方もあります。 確率で出す場合は、二値の場合の発展版です。
因果効果 という呼び方をしますが、「処置あり・なしの差」という量的な指標で評価することもできる理論です。 この場合は、結果系の変数は量的変数です。 「売上」や「血圧」のような項目が使えます。
順路
次は
d分離
