検証したい原因系の変数が量的変数の因果推論

第3変数の除去（原因系が二値）では、統計的因果推論で中心的な方法になっている２つのアプローチを説明していますが、タイトルにあるように、原因系が二値の場合です。より正確には、効果の有無を検証したい原因系が二値の場合です。

「この施策は効果があるのか？」、「この施策の効果はどの程度か？」といった検証に使う方法なので、「施策あり・なし」の二値の方法になっています。

因果推論の必要な場面では、検証したい原因系の変数が二値ではなく量的変数のことも多いです。そのような場合の手法が、このページになります。

d分離

causal_effect
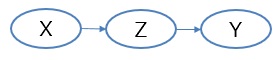
第3変数の除去（原因系が二値）の内、 d分離の方については、Zが二値以外にも応用できます。

YにZだけでなく、Xの効果も含まれていて、
Y = A1 * Z + A2 * X + B
という回帰式で値が精度の高いモデルになるのなら、A1がZの因果効果を表しています。

Zが二値の時は、A1は、「処置あり」と「処置なし」の差で、因果効果の値を表しますが、 Zが量的変数の時は、Zが１単位あたりの因果効果を表します。例えば、Zの単位がメートルなら、A1は、「１メートル当たりの因果効果」という意味にになります。

第3変数の除去（原因系が二値）の内、反事実を使う方法については、量的変数に拡張できるのかが、筆者にはわかりません。拡張できれば、面白いのですが、できないような気がします。

二値の場合は、事実と反事実の２つを考えれば良かったのですが、量的変数となると、事実以外は無数にあります。これをどう扱うかがポイントなのですが、よくわからないです。