潜在変数で原因系の仮説作成

X1、X2、X3の変数があり、原因系とします。 Y1、Y2、Y3の変数があり、結果系とします。

このページの方法は、結果系の変数だけから、「原因系はどうなっているのか？」ということを調べる方法です。

方法の考え方

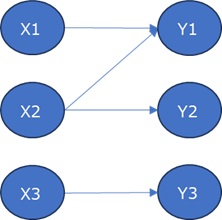
correlation
上のグラフのような構造をしているデータで考えます。矢印は、誤差を加えることを表しています。例えば、Y1は、X1とX2の線形和に誤差が加わったものです。

このようなデータの結果系のY1、Y2、Y3だけについて、因子分析をします。ここでは、独立成分分析を使っています。
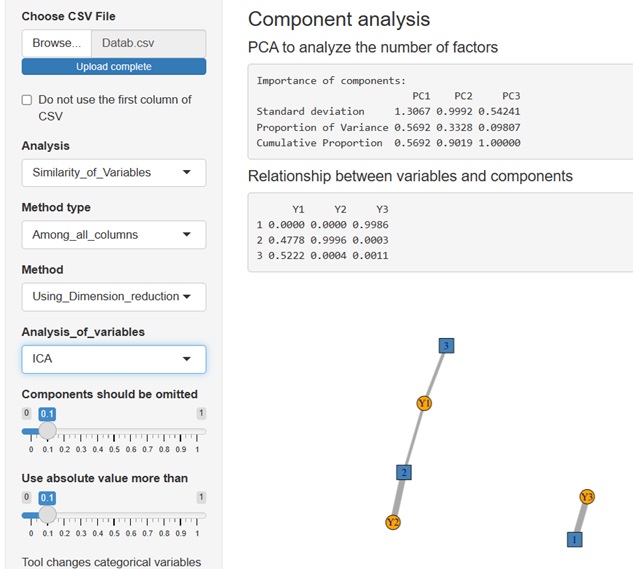
correlation

すると、独立成分（潜在変数）が３つ求まるのですが、求まった３つの潜在変数は、ちょうど、X1、X2、X3と同じ構造として求まっています。

結果系の変数と潜在変数の関係を見ることで、原因系の変数がどうなっているのかを考察することができるようになります。

ハイブリッド有向相関分析などに進んで、原因系と結果系の関係を直接的に調べる方法もありますが、純粋に結果系から推測される原因系と、実際の原因系のデータを比べると、データと事象の関係の理解が深まります。

上の例では、結果系だけについて、因子分析をしていましたが、原因系だけについて、因子分析をすると良い場合もあります。

原因系だけについて、因子分析をすると、原因系のさらに原因系を調べられます。

原因系の変数同士が、潜在変数を共有しているかを調べられます。

上記の例は、 R-EDA1 でしています。