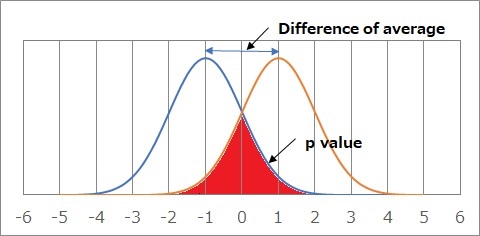
標準偏差が0の正規分布が2つあって、平均値が2ずれている場合が上の図です。 正規分布の差の検定2では、赤くした部分の面積を、p値と考えます。
差による分布の重なりの検定は、 データ全体の差の検定 の一種です。
差による分布の重なりの検定は、実際のデータに対して、統計学的な分布で近似して計算する点や、p値(確率)を計算する点は、統計学的な 検定 の方法と同じです。
また、判別の正誤の割合で判定する点は、 判別分析 のような ラベル分類 の方法と同じです。

標準偏差が0の正規分布が2つあって、平均値が2ずれている場合が上の図です。
正規分布の差の検定2では、赤くした部分の面積を、p値と考えます。
差による分布の重なりの検定では、実際のデータで作ったヒストグラムについて、2つの分布の重なり合っている部分を計算するのではなく、 実際のデータから作った確率密度関数で分布を近似して計算します。
こうすることで、2つの分布のサンプル数が大きく違っていても影響がないですし、データが少ない時に起きるデータの粗さの影響を小さくできます。
EXCELの場合、例えば、差が2の場合、下の式でp値が求まります。
=NORM.DIST(-1,0,1,TRUE)*2
「-1,0,1」という数字ですが、 -1の「1」は、「差が2の半分」から決まっています。0は平均値が0の分布であることを表し、一番右の1は、標準偏差が1という意味です。
等分散ではない場合、つまり標準偏差が異なる場合は、 EXCELで簡単に求める式は作れないので、 数値積分をするしかないようです。 計算の仕方としては、短冊のY方向の長さは、 それぞれの位置で2つの分布の確率密度関数を計算して、 小さい方を採用することで求まります。
順路


 次は
平方和分析
次は
平方和分析

