トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
管理図 は、ただの 折れ線グラフ ではなく、異常を判定するための方法が研究されて来ています。
例えば、下のグラフは、実測値と危険ラインを示したものです。
品質管理の場合は、危険ラインは、良品と不良品の判定基準になることがあります。
また、リスク管理では、このラインを超えると原因調査と対策が必要な基準になります。
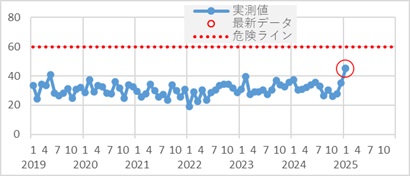
この例の場合は、危険ラインを超えてないので、「正常の範囲内」という結果になります。
管理図の第一歩は、危険ラインを使うものですが、「異常判定ルール」と呼ばれるものが考案されています。 管理限界線は、 外れ値検知 に活用できます。連は、 変化点検知 に活用できます。
下の例の場合、約30を中心にして、ランダムにばらついているので、 ホワイトノイズモデル が当てはまります。
グラフは、予測値の中心と、3シグマの範囲も示しています。
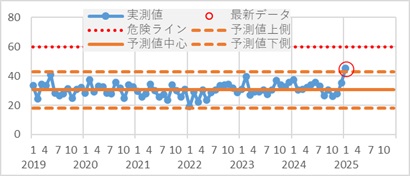
最新データは、予想値の上側よりも上になりました。危険ラインは超えていませんが、この判定方法では「異常」と判定します。
この方法は、最新データよりも過去のデータを使って、最新データの範囲を予測しています。 次のデータのばらつきによる異常の予測の方法を応用しています。そして、予測した範囲と実際のデータを比べて、判定しています。
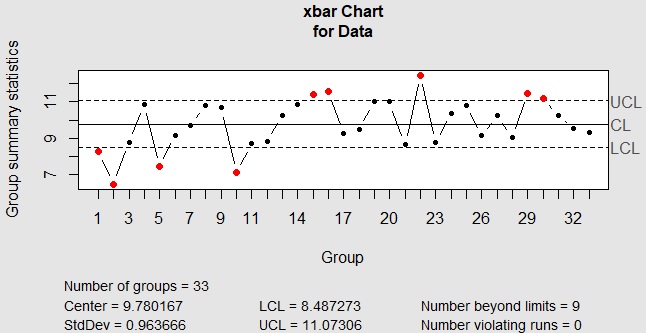
３シグマの範囲を表す線は、UCL（Upper Control Limit）、LCL（Lower Control Limit）と呼ばれます。
この管理限界線は、合否判定値や、危険の範囲等とは別物で、
あくまで、統計学的な計算値です。
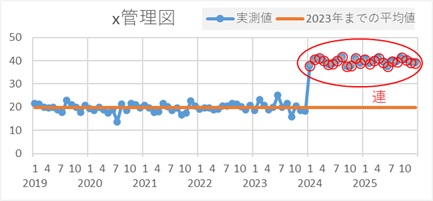
連は、「何かが変わった」という、 変化点検知 の目安になるので、知っておくと良いです。
下のグラフは、連の例です。2024年以降は、連続して予測値の中心よりも高い値が続いています。 ランダムに値が決まっているのなら、中心線よりも高くなる確率は、0.5（50%）です。中心線よりも連続して2回高くなる確率は、0.52なので0.25（25%）です。 連続して10回なら、0.510となり、0.001（0.1%）の確率でしか起きないことが起きたことになります。
中心線を境にして、どちらか一方の側に連続して値が続く状態を「連」と言います。連は、中心線が移動してしまう現象が起きたことを検知するための指標になります。
3シグマを超える確率が0.3%です。8回連続する確率が約0.4%で、9回連続する確率が約0.2%です。そこで、3シグマと目安を同じにするのなら、「連続9回以上」というのが連の発生の目安になります。
筆者の経験になりますが、3シグマ以外は、実際に使われることがなく、知られていないです。
異常判定ルールは、系統誤差がないように完璧に管理されて、偶然誤差しかない状態を想定して、「完全にランダムに発生するデータなら、あり得ないこと」を確率論を使って求めています。
ところが、実際の工場のデータは、異常値にならないように、人工的に制御されたデータです。 「値がだんだん上がって来たから、下がるように少し調節しよう」といった感じです。 つまり、偶然誤差ではなく、系統誤差が支配的です。 統計的に理想的な状態ではないです。
そのため、異常判定ルールで判定すると、異常ばかりになってしまって、現実的ではないです。 異常判定ルールが「異常」と考えているものも含めて、正常状態なのが、工場の実際の管理です。
例外として、3シグマについては、危険ラインと使い方が似ているので馴染みやすいですし、危険ラインではわからないことがわかるので、実務で使われています。 また、連は、 変化点検知 の分析で役に立ちます。
順路
次は
管理図の種類
