外れ値検知

異常検知
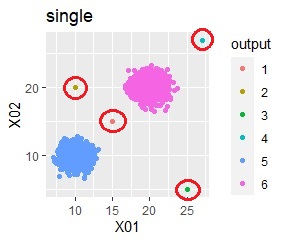
例えば、上のグラフで赤い円で囲ったサンプルは、大多数のサンプルのある２つのグループのどちらでもないので、外れ値です。

外れ値検知では、「外れていれば、異常」と考えて「このデータは外れ値かどうか？」という問題を扱います。「外れ値検知　＝異常検知」となっている文献があるくらい、外れ値検知は、異常検知の中心的な存在です。

外れ値検知の種類

一口に「外れ値検知」と言っても、やりたいことによって方法が違います。２種類に分かれます。

この違いは、混同されやすいです。問題の違いと、アプローチの違いは、１次元データで確認すると良いです。１次元データの外れ値検知のページでは、２種類の違いを、１次元データで説明しています。

どのサンプルが正常なのかが、わからない時の方法です。このような時は、「外れ値が混ざっているかどうか知りたい」、「どれが外れ値になのかを知りたい」といった問題があります。

機械的に見つける方法は、外れたサンプルの探索にあります。

どのサンプルが正常なのかが、わかっている時の方法です。

まず、外れと正常の両方がわかっている時は、外れ値の原因分析をしたいことがあります。また、過去の外れと正常のデータを使って、外れと正常を分けるシステムを作りたいことがあります。

あるいは、過去の外れ値のサンプルはないものの、正常のサンプルはわかっているので、それを使って、外れと正常を分けるシステムを作りたいことがあります。

ラベル分類では、「２つのラベルのどちらか？」というのは、ポピュラーな問題です。ところが、２つのラベルが、「正常・外れ値（異常）」の場合、ラベル分類の方法の多くは、適していません。

また、「正常のサンプルしかない」というケースにも、ラベル分類の方法の多くは、適していません。

外れ値と正常値を分けるモデルは、１クラスモデルが合っています。

下の例のデータの場合、赤い円で囲ったデータは、全体の増減の範囲の中なので、その意味では外れていませんが、SINカーブのような曲線からは明らかに外れています。
異常値

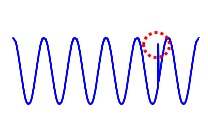
このような場合でも、データに何らかの加工をして、 外れ値として扱えるようにしてしまうのが外れ値検知のアプローチです。

このデータの場合は、「SINカーブ」と仮定することができます。この場合は、「SINカーブだったら、この時はこの値になるはず」という予測値が計算できます。その予測値との差を計算すると、外れ値として扱うことができるようになります。

また、このデータの場合は、1ステップ前や1ステップ後のデータが近いです。自己相関が高いことになります。「1ステップ前のデータ」との差を計算すると、外れ値として扱うことができるようになります。

以下の３つのページは、外れていないけれども外れている場合の方法です。