個々のサンプルの因果推論

個々のサンプルの因果推論は、統計的な因果推論の中でも、新しい分野です。

この分野は、 AIの説明可能性・解釈可能性の技術の方法としての方が、有名です。その応用として、統計的因果推論の方法としても使えます。

変数間の因果推論との違い

変数間の因果推論というのは、「この変数の値に影響しているのは、この変数だ」ということを調べるための方法です。「因果推論」や「統計的因果推論」と呼ばれている分野では、変数間の因果推論の方法が研究されて来ています。一般的に、「因果推論」や「統計的因果推論」と言えば、変数間の因果推論の話だけです。

このサイトでは、変数間の因果推論として、定量的な仮説の探索として、相関関係の探索、有向グラフになるデータの構造、因果の時間差というページがあったり、具体的な手法としては、重回帰分析、グラフィカルラッソ、 LiNGAM のページがあります。

これに対して、個々のサンプルの因果推論は、「このサンプルの値に影響しているのは、この変数だ」ということを調べるための方法になっています。

AIの説明可能性・解釈可能性として使われていると書きましたが、AIでは、例えば、「この画像を異常と判定したのは、この領域です」ということがわかるようになるための方法として使われます。

因果推論だと、異常状態の工程解析が使い道として考えられます。

変数間の因果関係を調べる方法でわかるのは、全サンプルに共通して言えるよう変数間の関係になります。例えば、「暑い日は、電気の使用料が増える」と言った特徴です。

個々のサンプルの因果推論でわかるのは、例えば、「暑くないのに、電気の使用料が増えた理由」があります。

異常の原因となる変数が、いつも同じ場合は、変数間の因果関係を調べる方法の方が、わかりやすいです。

逆に、異常の原因となる変数に、いろいろなパターンがある場合は、個々のサンプルについて調べる方法でないと、調べられないです。特に「そのサンプルの時だけは、この変数が異常だった」という場合は、個々のサンプルについて調べていないと、見落としやすくなります。

変数間の因果推論の方法の応用では、多次元空間の中での、調べたいサンプルの位置が、調べたいサンプルの特徴としての情報になります。

SHAPでは、目的変数との関係という観点で、調べたいサンプルの特徴がわかります。

変数間の因果推論の方法を、個々のサンプルの因果推論に応用します。

この応用に使えるのは、ラベル分類の方法で、決定木や MT法等があります。

これらの方法で、調べたいサンプルのラベル（目的変数の値）を例えば、「NG」として、それ以外を「OK」とすると、調べたいサンプルと、それ以外のサンプルの違いを調べることができます。

決定木だと、サンプルがどこの葉に分類されて、その葉がどのように分岐して作られているのかがわかるので、個々のサンプルの因果推論ができます。

決定木以外の方法の場合は、変数の重要度の分析をして、調べたいサンプルに影響のある変数を調べます。

SHAPは、個々のサンプルについて、目的変数の値に対して、重要な説明変数を調べる方法になっています。

目的変数も、説明変数も、量的データな時に使える方法です。

SHAPは、重回帰分析、決定木、ニューラルネットワーク、等の機械学習のモデルの中で、特定のサンプルの目的変数の値について、どの説明変数の影響が大きいのかを調べる方法になっています。

Rによる個々のサンプルの因果推論は、 Rによる個々のサンプルの因果推論にあります。
Shap値 Shap値

「機械学習を解釈する技術　予測力と説明力を両立する実践テクニック」　森下光之助　著　技術評論社　2021
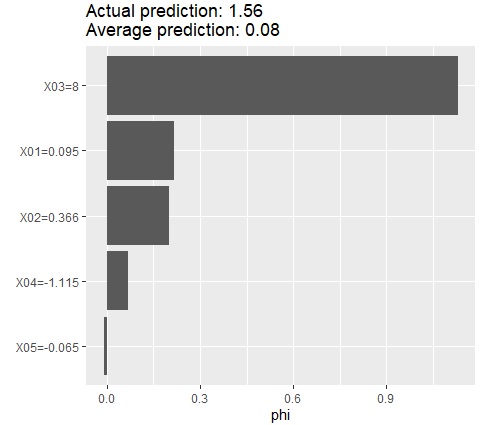
ICE・SHAP：個々のサンプルの予測値について、変数の重要度を評価する方法。