トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
アイソレーションフォレスト（IsolationForest）は、 外れ値検知 に特化した方法です。 外れ値かどうかだけを見分けます。
このサイトでは、出力が似ていることから、 クラスター分析による外れ値の検出 の一種として分類していますが、一般的には、 クラスター分析 として紹介されないです。
クラスター分析 や 近傍法 では、サンプル間の距離で近さを判断しますが、アイソレーションフォレストは距離を使いません。 その代わりに、「距離が離れていれば、こうなっているはずだ」ということを使います。
下のグラフでは、１点だけが外れています。
このようなデータの場合、縦でも横でも良いので、真ん中当たりで１本直線を引くと、外れ値とそれ以外を分けられます。
外れていない方のグループについては、直線で分けるには、たくさんの線が必要になります。
このように線を引くアプローチは、
決定木
と同じなので、決定木の一種でもあります。
アイソレーションフォレストでは、「簡単に分離できるサンプルほど外れている」と考えることで、外れ値を検出します。
距離を使う方法では、サンプル間のすべての組み合わせに対して距離を計算するので、計算量が大きいです。
一方、アイソレーションフォレストは、一度学習してしまえば、あとは引いた線のどちら側なのかを調べるだけで、外れ方が計算できます。 そのため、高速計算に適しています。
アイソレーションフォレストは、現実の課題に活用しにくい方法です。 線のどちら側なのかを調べるだけなので、線からどれくらい離れているのかは無関係です。 明らかに外れているサンプルの判定では問題がないのですが、あいまいな領域に対して、精度が低いです。
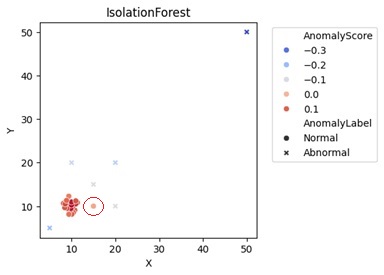
例えば、下の例では、右上の明らかに外れているサンプルは、「×」なので、外れ値として検出できています。 10,10あたりを中心にして、塊があり、その周りに外れているサンプルが６個ありますが、これらのうち５個は、外れ値として判定され、１個は正常値として判定されています。
６個全部を外れ値とするか、あるいは正常値とするかにした方が良さそうですが、そのような結果にはならないです。
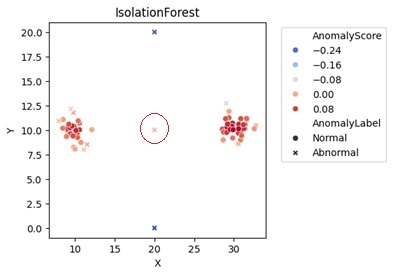
下の例では、まず、真ん中に縦に並んだ３つの外れ値が、正しく検出されているのは良いのですが、それらの真ん中のサンプルは、スコアが正常値の集団とあまり変わりません。
また、正常値のグループが、左右に２つ並んでいるように見えますが、正常値のグループの中にも外れ値が検出されています。
順路
次は
クラスター分析による予測
