トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

21世紀の、対応のある平均値の差の検定

21世紀の検定 としての、 対応のある平均値の差の検定 を、このページで整理します。

手順

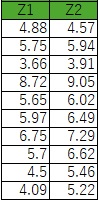
対応のある検定 の復習になります。 対応のある検定 は、 平均値の差の検定 の一種で、下のようなデータがあった時に、Z1とZ2という２つのグループの、それぞれの平均値に差があるかを調べます。 その時に、データの各行は対応があるとします。 例えば、「各行は同一人物のデータ」といった場合です。

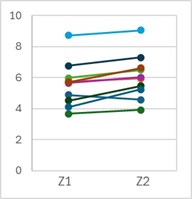
対応のある検定 では、「Z2 - Z1」というように、各行の差Yを計算します。

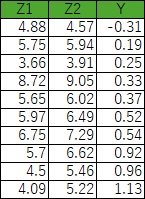
この後、 対応のある検定 では、 平均値の検定 をします。 Z2がZ1よりも大きければ、Z2-Z1のほとんどは、0よりも大きくなるはずなので、 「Z2-Z1の平均値は、0よりも大きいと言えるか？」という問題として扱います。

同様にして、対応のある平均値の差の検定のo値では、この後は、 21世紀の、平均値の検定 の手順になります。

検定対象

１つのグループの平均値と基準値の差です。 基準値を０にして、「平均値は、０か？」という使い方が多いです。

検定対象の信頼区間

平均値の差の検定では、信頼区間が下記の式になっています。

平均値差の信頼区間の下側の具体的な計算は、以下になります。 D1セルに平均値の差、N1セルにサンプル数、S1セルに標準偏差、を入力しておくと、以下の関数はコピペで使えます。
d1　：　平均値 - 基準値
n1　：　サンプル数
s1　：　標準偏差

=d1 - T.INV.2T(0.05,n1) * s1 / SQRT(n1)

p値

以下のどちらの関数でも、同じp値が求まります。

=T.DIST.2T(d1/ s1 / SQRT(n1)), n1)

p値の信頼区間

P値の信頼区間 は、p値を求める式に、平均値の信頼区間の下側を入れます。

平均値の信頼区間の下側をD2セルに入力しておくと、以下の関数はコピペで使えます。

=T.DIST.2T(d2/ s1 / SQRT(n1)), n1)

効果量

平均値の検定の効果量は、平均値と基準値の差を、標準偏差で割った式です。

=d1 / s1

効果量の信頼区間

効果量の信頼区間 は、平均値の信頼区間との対応から、以下で良いと筆者は考えています。

=d1 / s1 - T.INV.2T(0.05,n1) / SQRT(n1)

寄与率

寄与率 は、 平均値の差の検定の寄与率 の応用で、以下のようにして計算すれば良いと、筆者は考えています。

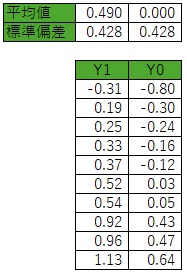
元のデータをX1という変数にして、平均値を引いたデータX0を作ります。 X0の平均値は０になります。 標準偏差は、変わらないです。

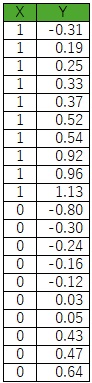
データを一列に並べて、新たにXという変数を作り、Xの値でY1とY0を区別できるようにします。

ここまで準備できると、ここからは、 平均値の差の検定の寄与率 と基本的に同じです。 相関係数rを求めます。

寄与率は、相関係数の二乗です。
=r1^2

近似曲線の機能を使うと、相関係数の二乗をグラフの中に、表示させることもできます。

寄与率の信頼区間

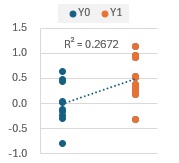
o値の信頼区間（上側）です。 相関係数の信頼区間 を使います。

=( ( EXP(LN( (1+R1)/(1-R1) ) -2*1.96/SQRT(n1-3) ) -1) / ( EXP(LN( (1+R1)/(1-R1) ) -2*1.96/SQRT(n1-3) ) +1) )^2

o値

平均値の検定のo値 のページにまとめています。

順路 次は 21世紀の、分散の比の検定