上の図は、AとBという２つのグループがあって、データが３つずつあります。
平均値の差の検定 が典型的ですが、一般に「対応あり」と書いていない検定の方法は、データの対応を使わない方法です。 検定の方法には、対応を使わない方法が多いです。 例えば、学校ごとにテストの平均点を計算して、その平均点の差を調べたい場合は、対応は気にしません。
「対応がある場合」というのは、例えば、 同じ学校の生徒の国語と数学の点数について、 「個人毎の国語と数学の点数の差は、どのくらいあるのか？」、といった調査です。 国語と数学の点数について、「個人」で対応があります。
他には、 2つの測定器を比較したい場合や、2つの実験条件を比較したい場合に、ペアになっているデータがある場合も当てはまります。
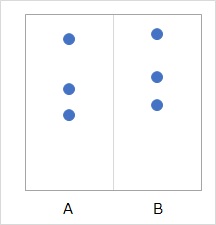
上の図は、AとBという２つのグループがあって、データが３つずつあります。
グラフを見る限り、「Bの方が平均値が高い」というのは、とても考えにくいです。 平均値の差の検定 をすると、P値が0.38になります。 普通、こういうデータの場合は、「Bの方が平均値が高いとは言えません。」という結論になります。
ところが、実は、上のデータは、同じ人について、AとBの条件で測ったデータで、それが３人分あったとします。
つまり、対応関係があったとします。
そして、対応関係をグラフに書き込むと、下の図のようになっているとします。
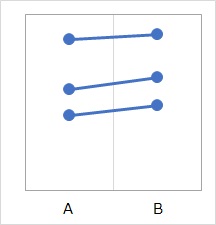
この場合に、対応のある平均値の差の検定を使うと、P値が0.03となり、とても小さいので、 「Bの方が平均値が高いとは言える。」という結論として、進められるようになります。
対応付けたグラフを見ると、個々のサンプルについては、Bの方が少し高いように見えます。 対応のある検定は、この特徴を調べる方法になっています。
もしも、「Bの方が高い」ということが事実なら、「B-A」は、どれも０よりも大きくなるはずです。 対応のある検定では、これを調べます。
まず、BとAの差（B-A）を計算します。
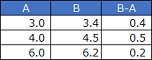
一般的な対応のある検定では、 平均値の検定を使って調べます。 以下、このページで「対応のある検定」と呼んでいるのは、平均値の検定を使う場合です。
平均値の検定を使う場合は、 「B-Aの平均値は、０よりも高いと言えるのか？」ということを調べようとします。
対応のある検定は、注意点があります。 ただし、注意点であって、弱点や欠点ではないです。
また、自分のやりたいことが、「対応のあるデータについて、片方のグループの方が平均値が高いと言えるのかを調べる」であるのなら、大した注意点ではないです。
一方、 「対応のあるデータについて、片方のグループの方が全体的に高いと言えるのかを調べる」、という目的で、この検定を使う場合は、重要な注意点です。 この目的に対して、この検定を使うと、事実とは反対の結論を導き出すこともあり、検証したいことの検証にならないので、重要です。
筆者の経験の範囲ですが、実務のデータ分析で、「平均値が高いと言えるのか」というケースはなく、 「全体的に高いと言えるのか」というケースが普通です。 「全体的に高いと言えるのか」を調べたいのですが、他に良さそうなものがないので、「平均値が高いと言えるのか」を採用しています。 （この状況を変えたくて考案したのが、分布のズレの検定です。）
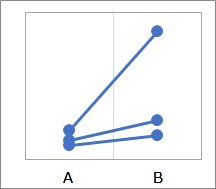
上の図の場合は、対応がある検定でも、対応がない検定でも、P値がだいたい0.13になり、「Bの方が平均値が高いとは言えません。」という結論になります。
個々の対については、Bの方が高いのですが、ばらつきが大きいために、「Bの方が高い」という結論が出ません。
この現象は、サンプル数が少ない場合に起きやすいです。
ちなみに、この例のような事は、筆者は実際に体験しました。 どの場合でも、Bの方が高いのに、対応のある検定をすると有意にならないので、「なぜ？」と考えました。 「B-Aのばらつきが大きいと、B-Aが全部０よりも大きくても、有意にならないことがある。」という事に気付くまでに、それなりに時間がかかりました。
対応のある検定は、 平均値の検定 の応用なので、サンプル数の影響を受けます。
サンプル数が多いと、全体的については（個々の対については）、Bの方が高いとは言い難いような場合であっても、「Bの方が高い」という結論になりやすくなります。
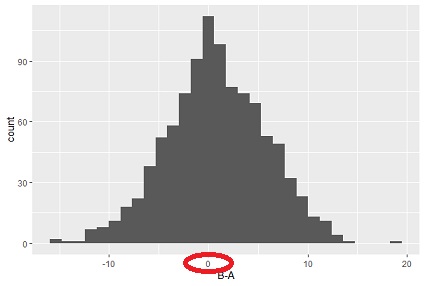
例えば、下の図は、対応のある平均値の差の検定で、「Bの方が高い」となる例です。 横軸は、「B-A」です。 B-Aの平均値が、0.8で、これに対して「０かもしれないと言えるか？」ということを調べて、「０かもしれないとは言えない」という結果になります。 P値は、0.00000017です。
グラフを見ると、０に対して、プラス側もマイナス側も同じくらいのサンプル数になっています。
このため、「平均値はBの方が高い」とは言えても、「全体的にはBの方が高い」とは言えないです。
サンプル数が多いと、こういう現象が起きやすくなります。
対応のある検定の注意点への対策としては、 B-Aを計算した後に、 平均値の検定 以外の方法を使うアプローチになります。
「対応のあるデータについて、片方のグループの方が全体的に高いと言えるのか」を調べるための方法としても使えます。
Rの実施例は、 Rによる違いの有無の分析 のページにあります。
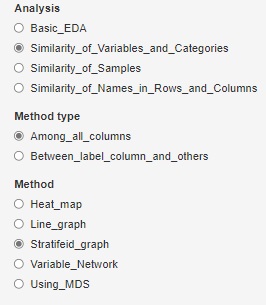
R-EDA1
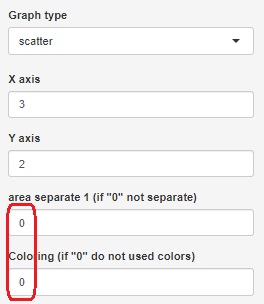
では「Stratifeid_graph」で、「scatter（散布図）」を選び、層別と色分けの変数を０にして指定しないようにすると、
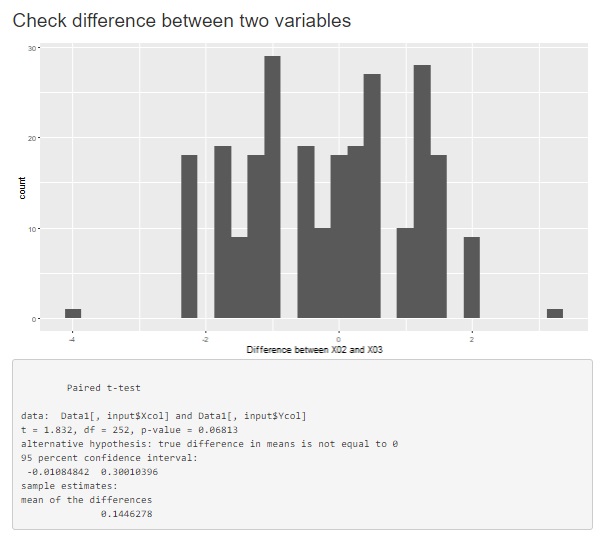
相関分析の下に、対応のある平均値の差の検定の結果が出ます。
順路
次は
スモールデータの検定の効果量
