品質管理 等の実務で、一番使われるのは、平均値の差の検定かと思います。
平均値の差の検定は、２つの母平均の差の検定が基本です。 これは、単純に２つの平均値を引き算した値についての検定です。
２つのグループがあって、平均値を比較したい場合、スチューデントのt検定と、ウェルチのt検定があります。
この違いとして、「等分散を仮定するかが違う。等分散を仮定するのがスチューデントのt検定」と呼ばれますが、筆者には、よくわからない点です。
式を見ると、いずれも、２つの分散と、２つのサンプル数を使って、合成した分布の標準誤差に相当するものを計算するのですが、その式が違っています。 この式の違いと、「等分散を仮定する・しない」と違いの関係が、わからないです。
使い分けるべきかは、不明な点がありますが、定説通りに使い分けるとすると、それはそれで難しいことがあります。
まず、等分散を仮定するかが違いだとすれば、「正確に使い分けるには、事前に 分散の比の検定 をする。」と考えたくなります。
しかし、「 分散の比の検定 をして、P値を見れば良い」というような単純な手順ではないので、あまり良くないです。
筆者としては、「メカニズムから考えると違いがあるはず」といった積極的な理由がない限りは、どちらでも良いと考えています。 どちらでも良いのなら、メジャーな方、つまり、スチューデントのt検定が良いと思います。
筆者の経験では、両者の使い分けが、問題解決の中で重要になったことはないです。
ただ、どちらを選ぶのかによって、p値と有意水準の大小が逆転することがあり、この大小関係に注目されることが多いので、注意して使うことはしています。
平均値の差の検定で、「平均値に差があると言えるのか？」ということをどのようにして調べているのかを、イメージでまとめると以下のようになります。
まず、例として使うデータは、標準偏差が１になっている２つのグループで、グループAの平均値が０で、Bの平均値が0.5です。
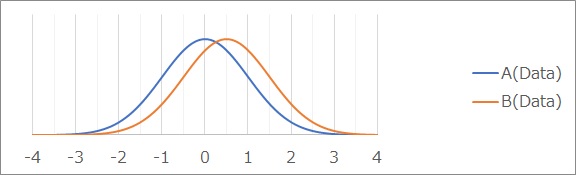
このグラフを見て、「差がある」ということは判断できませんが、平均値の差の検定も、このグラフから判定する仕組みにはなっていません。
平均値の差の検定では、平均値がある範囲を計算して、それを使って、平均値の差を判定します。
平均値がある範囲のグラフが下図になります。
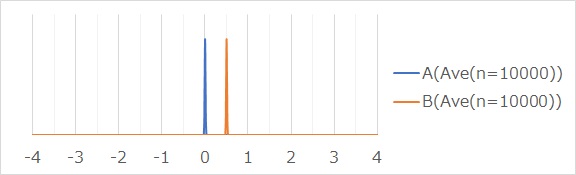
このグラフを見ると、２つの平均値の範囲が重ならないので、「平均値に明確に差がある」という判断ができるようになります。
平均値の差の検定で、調べる統計量は、ざっくり書くと、以下のようになっています。
平均値の差／（標準偏差／サンプル数nの平方根）
（標準偏差／サンプル数nの平方根）
という部分が分母にありますが、これは、
標準誤差
と呼ばれているものです。
標準誤差は、平均値の分布のばらつきの大きさです。
つまり、平均値の差の検定は、「平均値の差は、平均値の分布のばらつきが何個分か？」ということを、評価する方法になっています。
上の直観的な説明で、「２つの平均値の範囲が重ならない」という状況を、定量的に表すと、
平均値の差／（標準偏差／サンプル数nの平方根）
という量が、とても大きい、ということになります。
なお、上記では、わかりやすさを重視して、直観的な説明をしています。 しかし、平均値の差の検定を、２群のばらつきの問題として理解する説明は、一般的ではないです。
一般的な説明は、 平均値の差の検定の仕組み にあります。
分散分析 は、集団の数が２つより多くても使えます。 対応のある平均値の差の検定 は、２つの集団同士の個々のデータに対応がある場合に使えます。
なお、 分散分析 と 対応のある平均値の差の検定 には、「平均値の差の検定の変形版・発展版」以外の使い道が、それぞれにあります。
Rの実施例は、 Rによる違いの有無の分析 のページにあります。
Before-Afterを簡単に比べる方法としては、
R-QCA1
が良いかと思います。
１列目と２列目に比べたいグループのデータをそれぞれ入れたcsvファイルを用意して、読み込むとできます。効果量として、コーエンのdも計算されます。
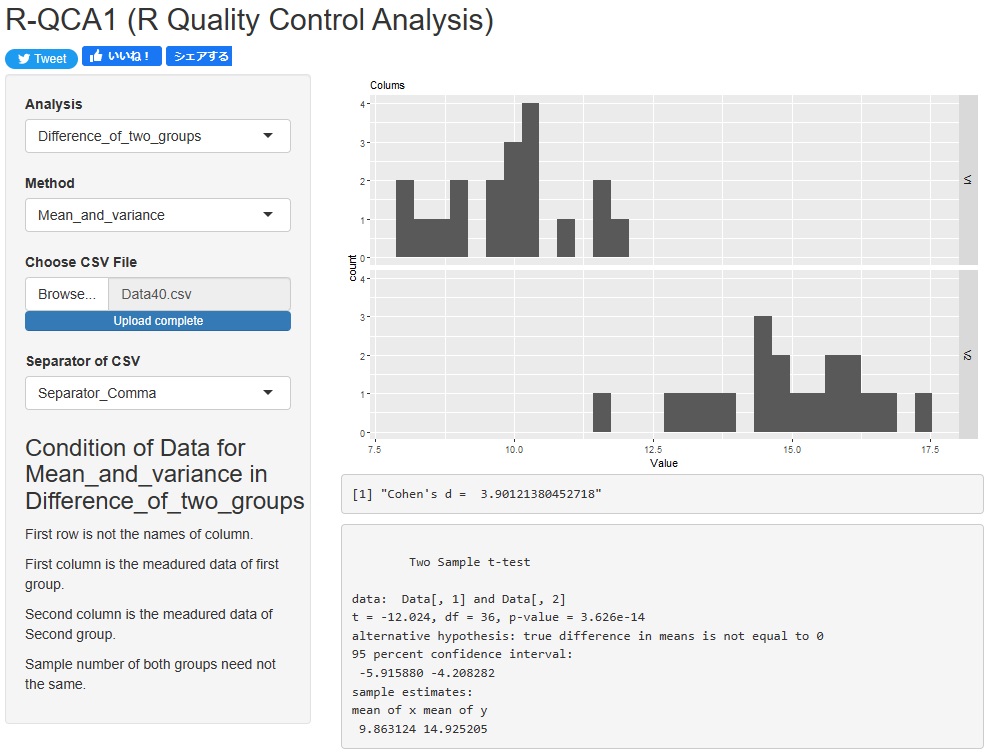
R-EDA1
では「Basic_test_All_Varaiables」を選ぶと、ラベルの変数を元に、各変数を層別して、すべての変数について、ラベルが０と１のグループの平均値の差の検定ができるようになっています。
p値だけが出力されます。
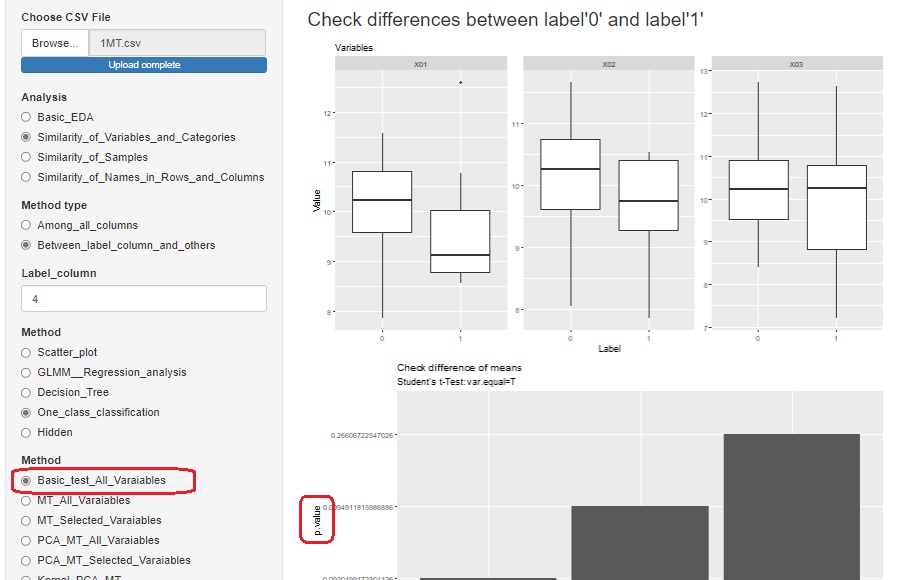
順路
次は
平均値の差の検定の、p値とサンプル数の関係
