平均値の差の検定 がありますが、このページのタイトルは、「ばらつきの違いの検定」としていて、「標準偏差の差の検定」にはしていません。
この理由は、まず 誤差の伝播 のページにもありますが、標準偏差同士は、足したり、引いたりできない性質があるので、数学的な意味での「差」という言葉が当てはまりません。 また、ばらつきの違いを見るのに、数学的な差ではなく、「比」を使います。
さらに、標準偏差は平均値と単位が同じになるので、ばらつきの尺度として理解しやすいのですが、 ばらつきを扱う検定では、検定の対象が分散になります。
２つのグループがあって、標準偏差の違いの有無を調べたい場合は、F検定があります。
平均値の差の検定 では、「２つのグループの分散が同じ（等分散）」という仮定のあるものがあります。 そのため、ばらつきの違いの検定は、「等分散性の検定」として、平均値の差の検定の前に使われることがあります。
複数のカテゴリについて、分散（ばらつき）が同じかどうかを調べるための検定のひとつが、バートレット検定です。
分散分析 には等分散の仮定がありますので、その検定に使われることがあります。
ちなみに、バートレット検定は、一元配置分散分析の等分散性の検定に相当するのですが、 多元配置分散分析（二元以上のもの）に対して、ばらつきの違いの検定はないようです。
実験データの解析 で、多元のものに対して、ばらつきの違いを分析する方法としては、 二段階設計 として 品質工学 が使っているものがあります。 ただし、検定ではありません。
Rの実施例は、 Rによる違いの有無の分析 のページにあります。
Before-Afterを簡単に比べる方法としては、
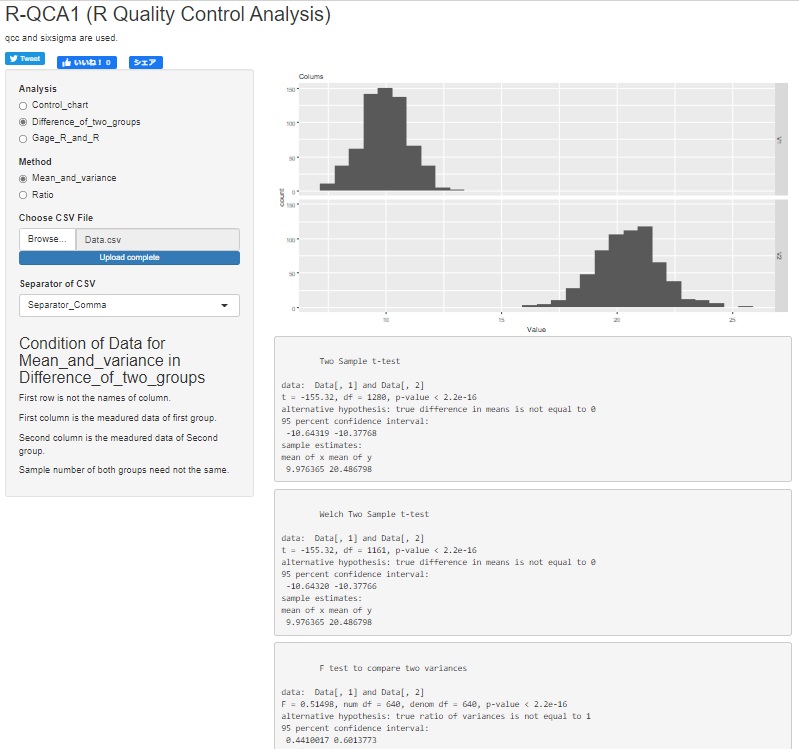
R-QCA1
が良いかと思います。
１列目と２列目に比べたいグループのデータをそれぞれ入れたcsvファイルを用意して、読み込むとできます。
平均値の差の検定の下に、分散の比の検定の結果が出ます。
R-EDA1
では「Stratifeid_graph（層別のグラフ）」を選んで、「histgram（ヒストグラム）」や「box_plot（箱ひげ図）」を選び、
層別のための変数が１個だけ選ばれた時には、
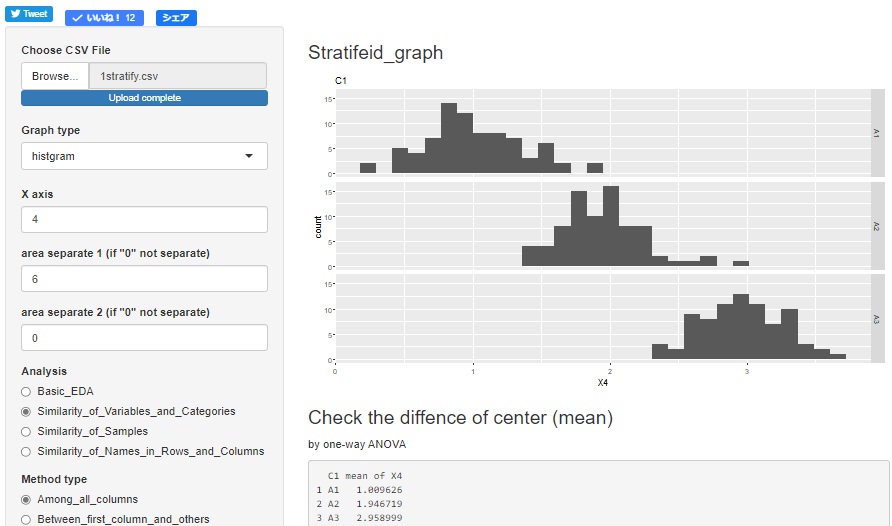
グラフを描くために選んだ変数を使って、バートレット検定ができます。
グラフの下に、分散分析の結果が出て、その下にバートレット検定の結果が出てきます。
R-EDA1
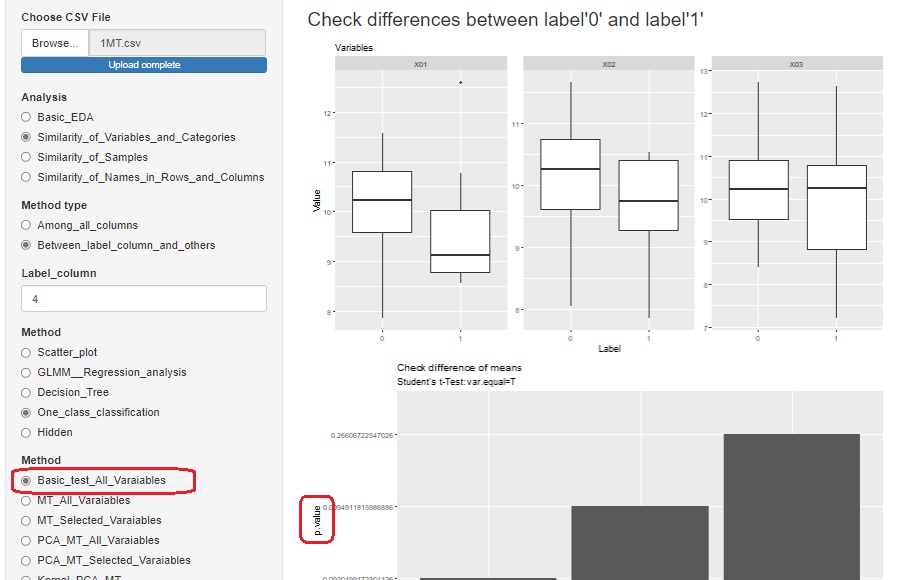
では「Basic_test_All_Varaiables」を選ぶと、ラベルの変数を元に、各変数を層別して、すべての変数について、ラベルが０と１のグループについて、
２つの母分散の比の検定ができるようになっています。
平均値の差の検定の下が、母分散の比の検定です。
p値だけが出力されます。
順路
次は
分散の比の検定でできないこと
