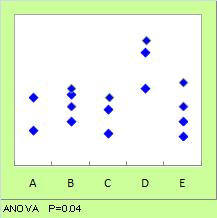分散分析（ANOVA ： ANalysis Of VAriance））は、 平均値に違いがあるかどうかを、ばらつきも考慮しながら判断するための方法です。
平均値の差の検定
は、他にもありますが、
分散分析は、比べたい平均値が２つより多い場合でも使えるので便利です。
分散分析（ANOVA ： ANalysis Of VAriance））は、 平均値に違いがあるかどうかを、ばらつきも考慮しながら判断するための方法です。
平均値の差の検定
は、他にもありますが、
分散分析は、比べたい平均値が２つより多い場合でも使えるので便利です。
分散分析は平均値の差を 検定 するために、分散を使っています。 分散を使って計算するので、「分散分析」という名前ですが、平均値の差を検定する方法です。ややこしいです。
分散分析は、 実験計画法 の分野で詳しく紹介されています。 そのせいか、分散分析が実験結果の解析方法として認知されていることもあるようです。 しかし、分散分析の本来の姿は、「２つ以上の平均値を、ばらつきも考慮して比べる方法」ですので、 実験のデータでなくても役に立ちます。
実験結果の解析で使う場合は、実験条件の違いによる平均値の差を検定するのに使われます。
分散分析では、まず、全体の分散を、各集団の平均値の分散と、各集団毎の分散（誤差の分散）に分けます。
次に、その２つ分散について、母分散の比の検定（F検定）をします。 それによって、平均値のばらつきが、同じ母集団から発生したものと言えるのかどうかを判断します。 つまり、このばらつきが有意であるなら、「平均値には差がある」という判断ができるようになります。
上記では、比べたい平均値が３つ以上ある場合でも使える 平均値の差の検定 の方法として、分散分析を説明しています。
その中で、分散分析は実験データの分析方法として紹介されることが多いと書きましたが、実験データには、「平均値が３個以上ある」ということだけでなく、 「因子が２個以上ある」ということもあります。
因子が複数ある場合が、 多元配置分散分析 です。
ややこしくなるので 計算方法のところで特に書きませんでしたが、 分散分析では、水準毎の分散は等しい、と仮定した計算になっています。 水準毎でばらつきが違っていても、考慮されていません。
仮定が成り立っていなくても計算はできますが、解釈には注意が必要です。
ばらつきの違いの検定 を一緒に実施して、この仮定が成り立っているのかを確認することもできます。
また、分散分析をする時は、データをグラフにして、どんなデータに対して出された結果なのかを確認した方が良いです。
データが多い時は
箱ひげ図
、
少ない時は
一次元散布図
が良いです。
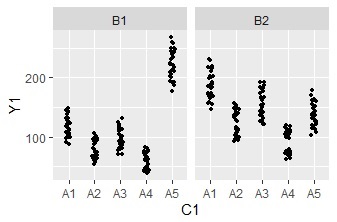
二元配置分散分析までなら、Excelのデータ分析の機能でもできます。
Rの場合は、このサイトでは、 Rによる違いの有無の分析 のページに実施例があります。
R-EDA1
では「Stratifeid_graph（層別のグラフ）」を選んで、「histgram（ヒストグラム）」や「box_plot（箱ひげ図）」を選ぶと、
グラフを描くために選んだ変数を使って、分散分析ができます。
「histgram（ヒストグラム）」は二元までですが、「box_plot（箱ひげ図）」では三元もできます。
質的変数の選んだ数によって、一元配置〜三元配置の使い分けが自動で行われます。
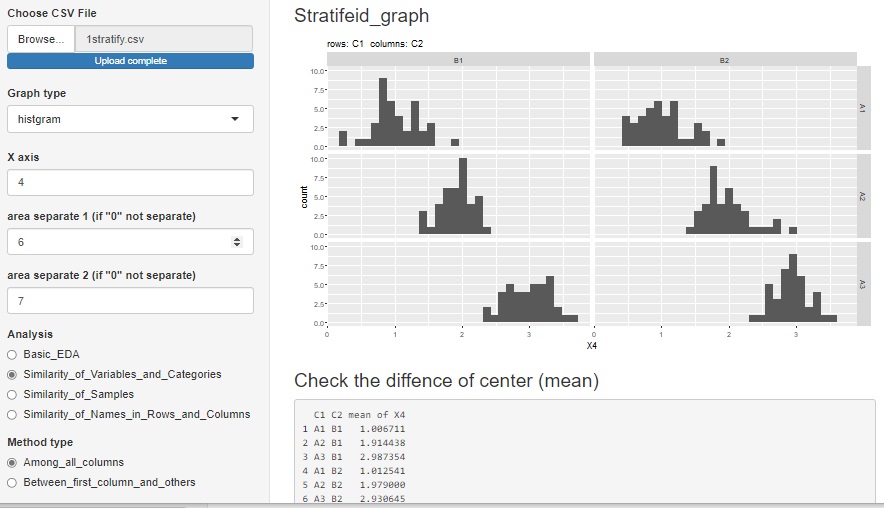
R-EDA1 で、三元以上の多元配置分散分析をしたい場合は、 一般化線形混合モデル の機能を使います。
目的変数が量的変数、説明変数が質的変数だけのデータで、 一般化線形混合モデル を実行すると、多元配置分散分析と同じになります。 R-EDA1 の 一般化線形混合モデル では、二次のフルモデル（交互作用ありのモデル）からスタートして、有意でない項は、取り除いたモデルが出力のなります。
また、 普通の分散分析では、誤差の分布として、正規分布が使われますが、 一般化線形混合モデル を使う、もうひとつの利点として、正規分布以外を使える点があります。 これによって、目的変数が計量値ではなく、計数値（個数などの、数えたデータ）の時に、誤差の分布として、ポアソン分布を使う分析もできます。
順路
次は
対応のある検定
Tweet
