分散の比の検定 用のo値です。
標準偏差の比dと、o値の関係が下の図です。
o値Bだけは、サンプル数によって、結果が変わります。 ここでは、2つのグループのサンプル数をいずれも10にしています。
いずれも比が1に近ければ1に近く、比0に近ければ0に近いです。
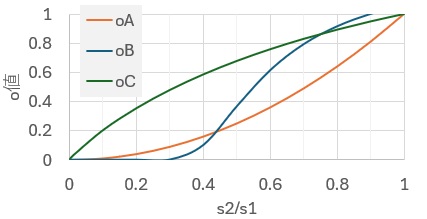
o値Bだけは、比が1に近い時に、o値が1より大きな値になります。
分散の比の検定のo値Aは、「小さい方の分散は、大きい方の分散の何割か？」という発想で、寄与率と似たものを求めることにしました。
= (S2 / S1)^2
ただし、s1 > s2
平均値の検定、平均値の差の検定、比率の差の検定は、検定統計量の構造が同じで、
平均値の差／（標準偏差／サンプル数nの平方根）
という形をしています。
分母は、
標準誤差
です。
従来からあるこれらの検定について、効果量は、
平均値の差／標準偏差
という形です。
この形にすると、
z検定
を応用できます。
分散の比の検定のo値Bも、このような作り方ができると良いのですが、 分散の比の検定 は、式の形が違うので、z検定が応用できません。
そこで、分散の比の検定を、 z検定 の形でやってしまう方法を考えました。 その方法については、 z検定による分散の比の検定 のページにまとめています。 そして、そこから、o値を求めるための検定を導き出すことにしました。
平均値の検定と、その効果量の検定（平均値の検定のo値B）とのアナロジーで考えると、分散の比の検定のo値Bは、下表になると考えました。
分散の比の検定のo値Bが、上の式で定式化できるとすれば、各種の評価指標のEXCEL関数は、 比率分布の差の効果量の検定 と同様にして、以下のようにして求まるはずです。
以下のEXCELの計算式では、以下のようになっています。
s1 ： 変数1の標準偏差
s2 ： 変数2の標準偏差
n1 ： 変数1のサンプル数
n2 ： 変数2のサンプル数
ただし、s1 > s2
任意のセルに、評価指標の計算式をコピーして、S1、S2、N1、N2のセルにこれらの数字を書いておくのが、一番簡単な使い方です。
NORMDIST関数の第１引数は、検定統計量です。 第２引数は、差がない事を基準にするので０です。 第３引数は、標準偏差です。
=(1 - NORMDIST( ( (s1/s2)^2 - n2 / (n2-2) ) / SQRT( (2 * n2^2 *(n1+n2-2) ) / ( (n2-2)^2 * (n2-4) ) ) , 0 , 1 ,TRUE)) *2
o値の計算の検定統計量の部分を、信頼区間の下限に変更します。
=(1 - NORMDIST( ( (s1/s2)^2 - 1.96*(SQRT( (2 * n2^2 *(n1+n2-2) ) / (n1 * (n2-2)^2 * (n2-4) ) )) - n2 / (n2-2) ) / SQRT( (2 * n2^2 *(n1+n2-2) ) / ( (n2-2)^2 * (n2-4) ) ) , 0 , 1 ,TRUE)) *2
分散の比の検定のo値は、下のグラフの赤い部分です。
２つの分布が重なっている部分の面積になります。
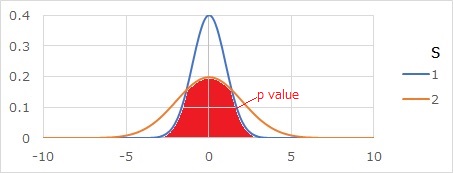
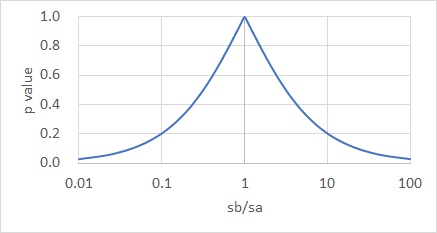
計算すると、下のグラフになります。
グラフの横軸は、２つの分布の標準偏差の比です。
２つの標準偏差が違うほど、小さな値になっています。
良く見る部分を拡大すると、下のグラフになります。
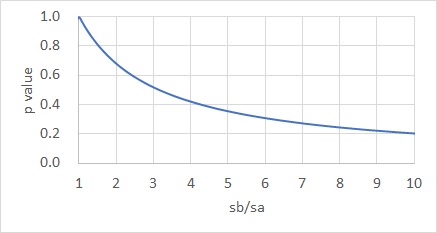
このp値は、一般的な検定のように、0.05を目安にするものではないです。 例えば、横軸が3の時に、o値は0.5くらいになりますが、「0.5(50％)もずれているから、２つのばらつきは違う、と考えられる」といった使い方になります。
２つの分布が重なっている部分の面積ですが、まずは、確率密度関数の曲線の交点xを求めます。
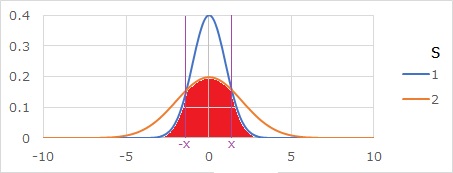
確率密度関数の式に代入すると、下の式になります。
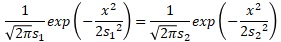
これを整理するとxの式が求まります。
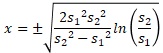
A2、B2というセルに２つの標準偏差が入力されている場合、EXCELでこのxを求める関数は、下記になります。
=-SQRT(2*B2^2*A2^2/(B2^2-A2^2)*LN(B2/A2))
上記のxを求める関数がD2というセルに書かれている場合、EXCELでo値を求める関数は、下記になります。
=2*(0.5-NORMDIST(D2,0,MAX(A2:B2),TRUE)+NORMDIST(D2,0,MIN(A2:B2),TRUE))
ここで、最初の「2*」という部分は、左側半分の面積だけを求めた式を２倍することを表しています。 「0.5」というのは、正規分布の左側半分の面積は、0.5なことを表しています。 MAX、MINというのは、２つの標準偏差の大小関係を間違えると、この式でp値が求まらないので使っています。 この関数だと、標準偏差がまったく同じ場合は、エラーになります。
順路
次は
21世紀の、分散分析
