平均値の検定のo値

平均値の検定用の o値を説明します。

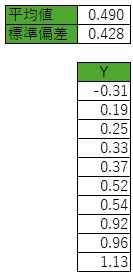
o value
以下の例では、上のような10個のデータがあり、「平均値は、０よりも大きいと言えるか？」を調べたかったとします。このデータの平均値は0.490、標準偏差は0.428です。

計算方法の違い

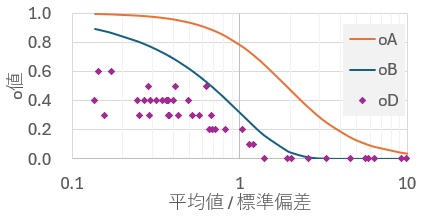
o値の違いが下の図です。

oAとoBについては、標準偏差が一定なら、平均値が小さければ１に近付き、大きければ０に近付く性質を持っていることがわかります。
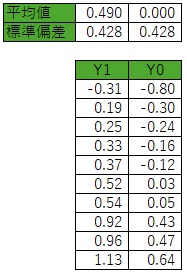
o value

o value
元のデータをX1という変数にして、平均値を引いたデータX0を作ります。 X0の平均値は０になります。標準偏差は、変わらないです。

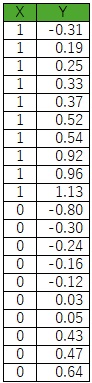
o value
データを一列に並べて、新たにXという変数を作り、Xの値でY1とY0を区別できるようにします。

ここまで準備できると、ここからは、平均値の差の検定のo値A と基本的に同じです。相関係数Rを求めます。
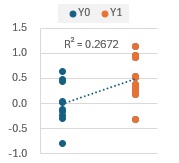
o value

=1- R1^2

上の例では、o値は、0.7328になります。

o値の信頼区間（上側）です。相関係数の信頼区間を使います。

=1-( ( EXP(LN( (1+R1)/(1-R1) ) -2*1.96/SQRT(n1-3) ) -1) / ( EXP(LN( (1+R1)/(1-R1) ) -2*1.96/SQRT(n1-3) ) +1) )^2

z検定を使うと、下の式でo値が求まります。
=(1 - NORM.DIST(0.49,0,0.428,TRUE)) *2

0、0.49、0.428の位置が異なっていますが、下の式でも、同じo値が求まります。これは、検定統計量にあらかじめ標準化をするかどうかが、違いになっています。
=(1 - NORM.DIST((0.49 - 0)/0.428,0,1,TRUE)) *2

o値の信頼区間は、 p値の信頼区間と同様に、効果量の信頼区間の上側と下側の値を、o値の計算式に入れて計算します。

下記は、信頼区間の上側の求め方ですが、下側でも同様です。

EXCELの場合、例えば、下の式でo値の信頼区間（上側）が求まります。nは、サンプル数です。
=(1 - NORM.DIST((0.45 - 0)/0.42 - 1.96/sqrt(n),0,1,TRUE)) *2

平均値の検定のo値Aは、簡単です。０以下のデータの割合を調べます。この例では、10個中1個なので、
o値　＝　0.1 （= 1 / 10）
です。

平均値の検定のo値Bは、分布を仮定して計算する必要がありますが、平均値の検定のo値Aは、何でも使えます。ノンパラメトリック検定の一種とも言えます。