 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
平均値の差の検定 のページにありますが、平均値の差の検定のp値は、平均値の差の有無だけを調べたい時の尺度になっています。
ところで、筆者の経験の範囲では、平均値の差の検定をする実務上の場面で、「平均値の差の有無だけを調べたい」ということは思い当たりません。 知りたいのは、「分布がずれていると言えるのか?」、「ずれは、どのくらいか?」ということなのですが、 それを知るための手段として、平均値の差の検定を使っているのが実状です。
そこで筆者が知りたいことを調べるための直接的な手段として考案したのが、このページで「平均値の差の検定のo値」と筆者が名付けた方法になります。 (世の中には、既に同じ方法があるかもしれないですが、筆者の知る限りではなさそうです。 もしあれば、名前はそちらに合わせるつもりです。)
コーエンのdと、o値の関係が下の図です。
いずれもコーエンのdが小さければ1に近付き、大きければ0に近付く性質を持っていることがわかります。
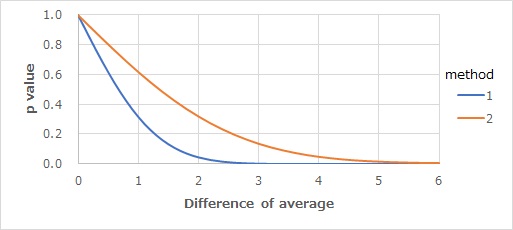
コーエンのdが1くらいの時に、3つの方法の違いが大きくなります。
下の例は、3つの例について、o値を計算してみたものです。 それぞれのグラフの上にある数字がo値です。
3つの例は、X2の平均値だけが違います。
それ以外は同じです。
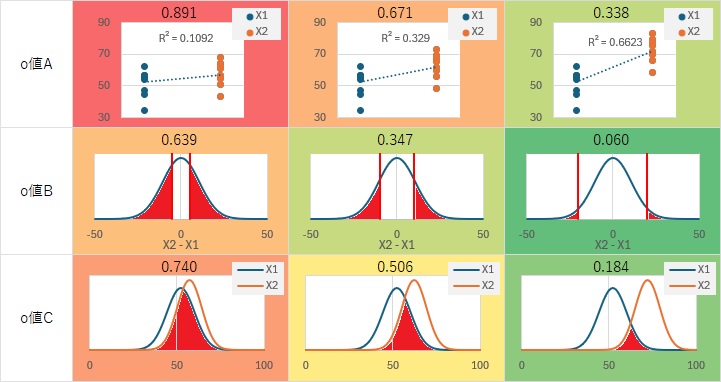
相関係数の検定のo値A と基本的に同じです。 説明変数を0と1の2値にすることで、相関係数を求めます。
=1- R1^2
o値の信頼区間(上側)です。 相関係数の信頼区間 を使います。
=1-( ( EXP(LN( (1+R1)/(1-R1) ) -2*1.96/SQRT(n1-3) ) -1) / ( EXP(LN( (1+R1)/(1-R1) ) -2*1.96/SQRT(n1-3) ) +1) )^2
平均値の差が2で、2つの分布の標準偏差がいずれも1の場合、o値Bは、下のグラフの赤い部分の面積の比率です。
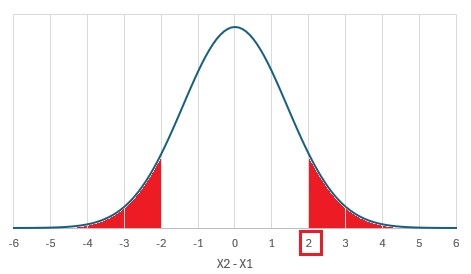
このグラフは、X2-X1の標準偏差から、X2-X1の分布を求めることで作っています。
X2-X1の標準偏差は、
平均処置効果と個別処置効果の関係
のページにある考え方を使うと、
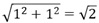
です。
D1、N1、N2、S1、S2のセルにそれぞれ値を書いておき、任意のセルに下記の関数をコピーするのが、一番簡単な使い方です。
EXCELの場合、例えば、差がd1の場合、下の式でo値が求まります。
=(1 - NORM.DIST(d1/sqrt((s1^2 + s2^2)),0,1,TRUE)) *2
sqrt((s1^2 + s2^2))
の部分は、
平均処置効果と個別処置効果の関係
の考え方を使っています。
o値の信頼区間は、 p値の信頼区間 と同様に、効果量の信頼区間の上側と下側の値を、o値の計算式に入れて計算すれば良さそうです。
下記は、上側の求め方ですが、下側でも同様です。
EXCELの場合、例えば、差が2の場合、下の式でo値の信頼区間(上側)が求まります。
=(1 - NORM.DIST(2 / sqrt(s1^2 + s2^2) - 1.96*sqrt(1/n1 + 1/n2),0,1,TRUE)) *2
ちなみに、o値の信頼区間の上側には、効果量の信頼区間の下側を使うので、「 - 1.96」という部分になっています。
平均値の差の検定のo値Cは、実際のデータに対して、統計学的な分布で近似して計算する点や、o値を計算する点は、統計学的な 検定 の方法と同じです。
また、判別の正誤の割合で判定する点は、 判別分析 のような ラベル分類 の方法と同じです。
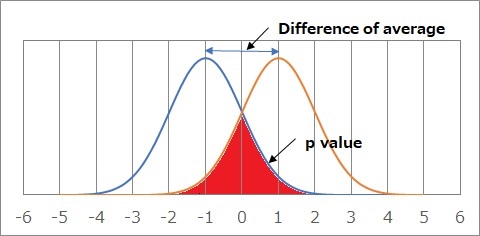
標準偏差が0の正規分布が2つあって、平均値が2ずれている場合が上の図です。
正規分布の差の検定2では、赤くした部分の面積を、p値と考えます。
平均値の差の検定のo値Aでは、実際のデータで作ったヒストグラムについて、2つの分布の重なり合っている部分を計算するのではなく、 実際のデータから作った確率密度関数で分布を近似して計算します。
こうすることで、2つの分布のサンプル数が大きく違っていても影響がないですし、データが少ない時に起きるデータの粗さの影響を小さくできます。
差がd1で、標準偏差がsの場合、下の式でo値が求まります。
=(1 - NORM.DIST(d1 / (2 * s), 0, 1, TRUE))*2
例えば、上のグラフのように、差が2で、標準偏差が1の場合、下の式でo値が求まります。
=(1 - NORM.DIST(1,0,1,TRUE))*2
等分散ではない場合は、標準偏差の平均値を計算にコーエンのdで使われている方法を使うことにして、以下で良いのではないかと考えています。
EXCELの場合、例えば、差がd1で、標準偏差がs1とs2の場合、下の式でo値が求まります。
=(1 - NORM.DIST(d1 / (2 * sqrt((n1*s1^2 + n2*s2^2) / (n1+n2))), 0, 1, TRUE))*2
「統計検定手法の改革...その3: 効果量, 信頼区間」 西井淳 2016
コーエンのdと、その信頼区間の紹介があります。
https://bcl.sci.yamaguchi-u.ac.jp/~jun/post/160605-effectsize/
順路


 次は
21世紀の、平均値の検定
次は
21世紀の、平均値の検定

