予測の方法としての、時系列分析と多変量解析の違い

このページでは、典型的な例として、 SARIMAXTモデルや三重指数平滑法を「時系列分析」として想定します。また、回帰分析、決定木などの教師あり学習の方法を「多変量解析」として想定します。

上記のように、時系列分析と多変量解析を分けます。両者は、予測の方法として使われることが一般的ですが、共通点と相違点があります。

入門的な方法による予測

時系列分析と多変量解析のいずれにも、入門的な方法がありますが、それについては共通しています。

例えば、下のグラフは、過去７日間の売上を表しています。このグラフだけを見て、８日目を予測するとしたら、「おそらく、平均の2200円くらいだろう。もしかしたら、1000円くらいかもしれないし、4000円くらいになるかもしれない。」となります。
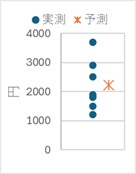
時系列分析と機械学習の違い

下のように折れ線グラフを作ると、時系列でデータを並べているので、時系列分析になりますが、このグラフを見て、「８日目は、過去７日間の平均で予測しよう」と考えるのなら、同じ予測になります。
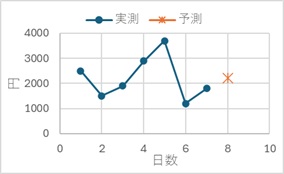
時系列分析と機械学習の違い

ところで、過去７日間のデータを折れ線グラフにして、下のグラフだとしたら、「おそらく、1000円以下だろう」と予測するのが自然です。
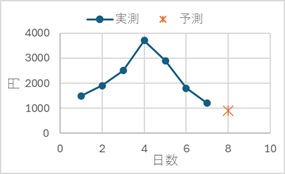
時系列分析と機械学習の違い

この折れ線グラフは、横軸が時系列を表す変数（日数）です。

この分析について、「売上と日数の、２つの変数を使った予測」と考えるのなら、多変量解析の一種です。「時系列の情報を使った予測」と考えるのなら、時系列分析の一種です。

上記は、解釈の違いはあっても、実際にやっていることは共通しています。下記は、両者の違いがあります。

多変量解析の立場では、時系列の変数は、様々な変数の中のひとつです。そのため、他の変数でも分析したり、様々な変数を組み合わせたりする場合もあります。

ちなみに、多変量解析では、「いつでも成り立っている法則」を見つけようとします。そのため、時刻のデータがあったとしても、モデルには含めないことが多いです。

上の例の場合、データは１日ごとで等間隔です。等間隔なので、「前日との差」を計算することができます。
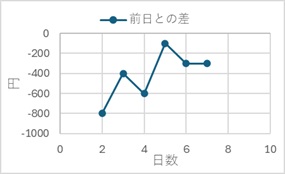
時系列分析と機械学習の違い

差を計算すると、直近は「-300」となっているので、この値を使って、「8日目は7日目よりも300円くらい下がるはず、だから、1000円以下になりそう。」という予測をすることもできます。

時系列分析には、「データは時刻の順に並んでいて、時間は等間隔になっている」ということを前提にして作られた理論があります。例えば、このサイトで時系列近傍法に分類した方法は、この系統の理論です。

ちなみに、「データは時刻の順に並んでいて、時間は等間隔になっている」という系統でも、時系列以外の変数を活用することがあります。例えば、 SARIMAXモデルの「X」の部分は、時系列以外の変数を表しています。