隣接行列の固有値分析 の中でも、有向グラフの場合です。
有向グラフの場合は、非対称行列になります。
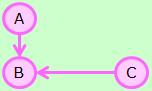
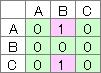
有向グラフの場合は、文献がないので、試しにやってみたのが、下記になります。
どのように活用したらよいのかがわからない結果でした。
まず、対角成分がすべて１の場合は、固有値がすべて１になり、対角成分がすべて０の場合は、固有値がすべて０になることがわかりました。
ひとつの要素に、複数の要素が集まるパターンの場合は、固有ベクトルに少数が表れ、そうでない場合は、0、1、-1だけになることがわかりました。
循環する構造があると、固有値、固有ベクトルが複素数になりました。
無向グラフの固有値分析 では、隣接行列を、直接、固有値分析するのではなく、ラプラシアン行列の固有値分析にすると、応用が広がっていて、「スペクトルグラフ理論」と呼ばれています。
スペクトルグラフ理論は、無向グラフの理論しかないようなのですが、試しに、有向グラフでもやってみたのが、下記の結果になります。 無向グラフの時のコードを、ほぼそのまま転用したら、うまく行ったのですが、有向グラフの時のように非対称行列では、「次数行列」や「ラプラシアン行列」という呼び方は、定義と合わないので、ここでは、「疑似ラプラシアン行列」としました。
結論としては、疑似ラプラシアン行列の固有値分析は、無向グラフの時のような結果になり、応用が利くようです。
有向グラフと無向グラフの大きな違いとして、固有値とグループの数の関係があります。
上の３つのグラフは似ていますが、上から２つ目までが、固有値０が１つで、３つ目だけ固有値０が２つあります。 つまり、３つ目は、「グループの数は２つある」という分析結果になります。
この違いは、疑似ラプラシアン行列を計算する前の、疑似次数行列の計算が原因です。
上の例の場合は、各行の合計値を、疑似次数とする計算方法になっています。
無向グラフの固有値分析 では、対称行列を使うので、次数を計算する時に、行の合計値にしても、列の合計値にしても、同じだったのですが、有向グラフの場合には違いが出て来ます。
グラフの矢印を、因果関係を表すものと考えるのなら、「原因が同じでも結果が異なるのは、２つの事象」と考えたいので、上の例のように、行の合計値を使った方が良さそうです。
条件付き独立になるデータの構造 を調べて、グラフに矢印をつける時は、矢の終点が集まる２番目の構造の時だけが区別できて、１番目と３番目は区別できないです。 これに合わせるのなら、列の合計値を使った方が良さそうです。
疑似ラプラシアン行列を使う方法は、 Rによる有向グラフの固有値分析 のページがあります。
順路
次は
A-B型の分析
