隣接行列の固有値分析 の中でも、無向グラフの場合です。
無向グラフの場合は、対称行列になります。
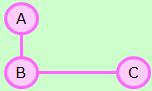
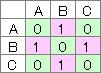
先に結論から書くと、相関行列の固有値分析と同じように進めた場合、あまり応用が利きません。
主成分分析 では、相関行列を固有値分析しますが、 無向グラフの場合は、それと同じような分析になるようです。
相関行列で、相関係数が０と１しかない特殊な場合になります。
例えば、下の例では、グループが３つありますが、、０にならない固有値は３つあるので、３つのグループになることがわかります。
上の例では、対角成分がすべて１になっています。相関行列を固有値分析する時と同じです。
ネットワークグラフでは、対角成分は、自己ループを表したり、その要素自身の大きさを表したりすることに使いますが、ここをゼロにした行列を固有値分析すると、意味不明の結果になります。
下の例では、A、B、Cと、D、E、Fがそれぞれグループなのは、上と同じですが、B-Cの結合と、E-Fの結合はないです。
このような隣接行列を固有値分析すると、意味不明の結果になりました。
隣接行列をAとします。
隣接行列の各行や、各列の和は、各頂点につながっている辺の数になりますが、これは「次数」と呼ばれます。 次数を対角成分にした行列は、「次数行列」と呼ばれます。
ラプラシアン行列は、次数行列をDとした時に、
L = D - A
で求まる行列です。
以下は、ラプラシアン行列の固有値分析の結果です。 グループの数と、固有値が０になる固有ベクトルの数が一致していることがわかります。
主成分分析
では、固有値が大きなものに注目しますが、この分析では、小さなものに注目する点が異なります。
「固有値が小さいもの ＝ 大域的な情報」という見方をするそうです。
Rによる無向グラフの固有値分析 のページがあります。
「グラフニューラルネットワーク」 佐藤竜馬 著 講談社 2024
グラフニューラルネットワーク
の専門書です。
スペクトルグラフ理論というものを紹介しています。その中で、無向グラフの場合の、隣接行列の固有値分析があります。
ラプラシアン行列がどのように出て来るのかの解説があります。
順路
次は
有向グラフの固有値分析
